分析:(1)当a=1且x>1时,构造函数m(x)=lnx+
-2,利用函数单调性和导数之间的关系即可证明:f(x)>3-
;
(2)根据函数最值和函数导数之间的关系将不等式恒成立问题进行转化,求实数a的取值范围;
(3)根据函数的单调性的性质,利用放缩法即可证明不等式.
解答:
(1)证明:要证f(x)>3-
,即证lnx+
-2>0,
令m(x)=lnx+
-2,
则m'(x)=
-=>0,
∴m(x)在(1,+∞)单调递增,m(x)>m(1)=0,
∴lnx+
-2>0,
即f(x)>3-
成立.
(2)解法一:由f(x)>x且x∈(1,e),可得a
>,
令h(x)=
,则h'(x)=
,
由(1)知lnx-1+
>1+
-=
>0,
∴h'(x)>0函数,h(x)在(1,e)单调递增,当x∈(1,e)时,h(x)<h(e)=e-1,
即a≥e-1.
解法二:令h(x)=alnx+1-x,则h'(x)=
-1=,
当a>e时,h'(x)>0,函数h(x)在(1,e)上是增函数,有h(x)>h(1)=0,
当1<a≤e时,∵函数h(x)在(1,a)上递增,在(a,e)上递减,
对?x∈(1,e),f(x)>x恒成立,只需h(e)≥0,即a≥e-1.---------------(7分)
当a≤1时,函数h(x)在(1,e)上递减,对?x∈(1,e),f(x)>x恒成立,只需h(e)≥0,
而h(e)=a+1-e<0,不合题意,-----------------------------------------------------------(8分)
综上得对?x∈(1,e),f(x)>x恒成立,a≥e-1.------------------------(9分)】
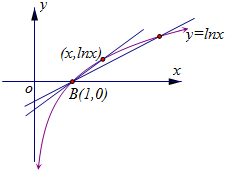
【解法三:由f(x)>x且x∈(1,e)可得
<由于
表示两点A(x,lnx),B(1,0)的连线斜率,
由图象可知y=
在(1,e)单调递减,
故当x∈(1,e)时,
>=,
∴0
<≤,
即a≥e-1.
(3)当a=
时,f(x)=
lnx+1,则
| n+1 |
 |
| i=2 |
f(i)=
ln(n+1)!+n,
要证
| n+1 |
 |
| i=2 |
f(i)>2(n+1-
),即证
| n+1 |
 |
| i=2 |
lni>2n+4-4
,
由(1)可知ln(n+1)>2-
,
又n+2=(n+1)+1>2
>
+,
∴
<,
∴ln(n+1)>2-
=2-4(-),
∴ln2+ln3+…+ln(n+1)
>2n-4[(-1)+-+…+-]=2n+4-4
,
故
| n+1 |
 |
| i=2 |
f(i)>2(n+1-
).得证.


 【解法三:由f(x)>x且x∈(1,e)可得
【解法三:由f(x)>x且x∈(1,e)可得





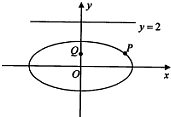 已知椭圆C:
已知椭圆C: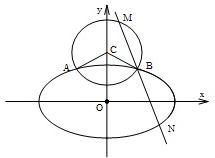 已知离心率为
已知离心率为 如图,F1(-c,0),F2(c,0)分别是双曲线C:
如图,F1(-c,0),F2(c,0)分别是双曲线C: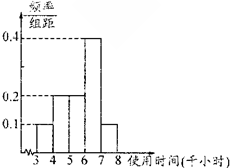 节能灯的质量通过其正常使用时间来衡量,使用时间越长,表明治疗越好.若使用时间小于4千小时的产品为不合格产品;使用时间在4千小时到6千小时(不含6千小时)的产品为合格品;使用时间大于或等于6千小时的产品为优质品.某节能灯生产厂家为了解同一类型号的某批次产品的质量情况,随机抽取了部分产品作为样本,得到实验结果的频率直方图如图所示.若上述实验结果中使用时间落入各组的频率作为相应的概率.
节能灯的质量通过其正常使用时间来衡量,使用时间越长,表明治疗越好.若使用时间小于4千小时的产品为不合格产品;使用时间在4千小时到6千小时(不含6千小时)的产品为合格品;使用时间大于或等于6千小时的产品为优质品.某节能灯生产厂家为了解同一类型号的某批次产品的质量情况,随机抽取了部分产品作为样本,得到实验结果的频率直方图如图所示.若上述实验结果中使用时间落入各组的频率作为相应的概率.