
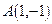
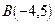
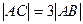
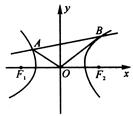
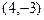 ,B
,B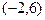 求点C使
求点C使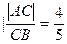 ;
;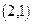 ,F2
,F2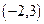 ,离心率e=0.8。求此椭圆长轴上
,离心率e=0.8。求此椭圆长轴上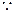 点C在AB延长线上,且
点C在AB延长线上,且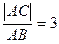 ,
,

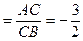 。
。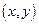 ,
,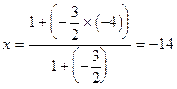
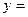
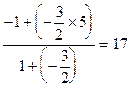 。
。 点C坐标为
点C坐标为 。
。
 可得
可得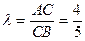 ,
,
 可得
可得 ,
,
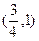 或
或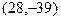
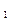 ,A
,A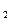 坐标分别为
坐标分别为
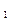 在
在 延长线上,A
延长线上,A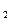 在
在 延长线上)
延长线上)


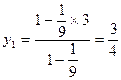
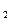 分线段
分线段 所成比
所成比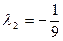 。可得
。可得
 点A
点A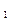 ,A
,A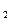 坐标分别为
坐标分别为 。
。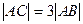 ,因此,可以知道比值
,因此,可以知道比值 ,代入线段的定比分点公式即可,对第(2)小题,应注意由
,代入线段的定比分点公式即可,对第(2)小题,应注意由 ,还不确定点C是在线段AB上,还是在线段BA的延长线上。因此,解此题时要考虑周到,不要丢解。对于第(3)小题,从题目表面还不能直接看出是求线段的定比分点问题,必须对椭圆的一些基本性质熟练掌握,应想到椭圆的焦点与长轴上两顶点的关系,及离心率的意义,才能给恰当地找出长轴上顶点分线段F1F2所成的比,才能求出长轴上两顶点的坐标。
,还不确定点C是在线段AB上,还是在线段BA的延长线上。因此,解此题时要考虑周到,不要丢解。对于第(3)小题,从题目表面还不能直接看出是求线段的定比分点问题,必须对椭圆的一些基本性质熟练掌握,应想到椭圆的焦点与长轴上两顶点的关系,及离心率的意义,才能给恰当地找出长轴上顶点分线段F1F2所成的比,才能求出长轴上两顶点的坐标。

 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案科目:高中数学 来源:不详 题型:解答题
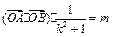 ,且满足2≤m≤4时,
,且满足2≤m≤4时,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com