
【题目】如图所示,在四棱锥![]() 中,底面
中,底面![]() 是
是![]() 且边长为
且边长为![]() 的菱形,侧面
的菱形,侧面![]() 为正三角形,其所在平面垂直于底面
为正三角形,其所在平面垂直于底面![]() ,若
,若![]() 为
为![]() 的中点,
的中点,![]() 为
为![]() 的中点.
的中点.
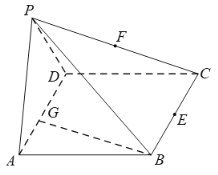
(1)求证:![]() 平面
平面![]() ;
;
(2)求证:![]() ;
;
(3)在棱![]() 上是否存在一点
上是否存在一点![]() ,使平面
,使平面![]() 平面
平面![]() ,若存在,确定点
,若存在,确定点![]() 的位置;若不存在,说明理由
的位置;若不存在,说明理由
【答案】(1)证明见解析(2)证明见解析(3)存在,当![]() 为
为![]() 的中点时,能使平面
的中点时,能使平面![]() 平面
平面![]()
【解析】
(1)利用已知可以判定四边形![]() 是平行四边形,利用平行四边形的性质可以得到线线平行,利用线面平行的判定定理证明出
是平行四边形,利用平行四边形的性质可以得到线线平行,利用线面平行的判定定理证明出![]() 平面
平面![]() ;
;
(2)根据![]() 为正三角形可以得到
为正三角形可以得到![]() ,再根据
,再根据![]() 是等边三角形得到
是等边三角形得到![]() ,这样根据线面垂直的判定定理可以证明
,这样根据线面垂直的判定定理可以证明![]() 平面
平面![]() ,再利用线面垂直的性质定理可以证明出
,再利用线面垂直的性质定理可以证明出![]() ;
;
(3)可以猜想![]() 为
为![]() 的中点时.根据已知侧面
的中点时.根据已知侧面![]() 垂直于底面
垂直于底面![]() ,可以通过面面垂直的性质定理可以得到
,可以通过面面垂直的性质定理可以得到![]() 平面
平面![]() .这样利用中位线可以证明出
.这样利用中位线可以证明出![]() 平面
平面![]() ,这样证明出猜想是正确的.
,这样证明出猜想是正确的.
(1)由已知,![]() ,
,![]() 所以四边形
所以四边形![]() 是平行四边形.
是平行四边形.![]() .
.
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() .
.
(2)连接![]() .
.![]() ,
,![]() .
.![]() 是等边三角形,
是等边三角形,![]()
又![]() ,
,![]() 平面
平面![]() .
.![]() .
.
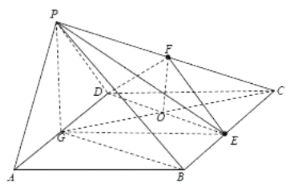
(3)当![]() 为
为![]() 的中点时,能使平面
的中点时,能使平面![]() 平面
平面![]() .证明如下、
.证明如下、
![]() 平面
平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() ,
,![]() 平面
平面![]() ,
,
![]() 平面
平面![]() .连结
.连结![]() 交
交![]() 于
于![]() .则
.则![]() 是
是![]() 的中点,
的中点,![]() .
.
![]() 平面
平面![]() .又
.又![]() 平面
平面![]() ,
,![]() 平面
平面![]() 平面
平面![]() .
.


科目:高中数学 来源: 题型:
【题目】给出下列命题:①等比数列1,![]() ,
,![]() ,
,![]() ,…(
,…(![]() )的前
)的前![]() 项和为
项和为![]() ;②等差数列
;②等差数列![]() 中,若
中,若![]() ,
,![]() ,则该数列的前13项或14项之和最大;③若等差数列
,则该数列的前13项或14项之和最大;③若等差数列![]() 公差为
公差为![]() ,则其前
,则其前![]() 项和
项和![]() ;④若等比数列
;④若等比数列![]() 单调递增的充要条件是首项
单调递增的充要条件是首项![]() ,且公比
,且公比![]() ;⑤若数列
;⑤若数列![]() 满足
满足![]() ,
,![]() ,则
,则![]() .其中正确的是______(把你认为正确的命题序号都填上).
.其中正确的是______(把你认为正确的命题序号都填上).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个不透明的箱子中装有大小形状相同的5个小球,其中2个白球标号分别为![]() ,
,![]() ,3个红球标号分别为
,3个红球标号分别为![]() ,
,![]() ,
,![]() ,现从箱子中随机地一次取出两个球.
,现从箱子中随机地一次取出两个球.
(1)求取出的两个球都是白球的概率;
(2)求取出的两个球至少有一个是白球的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() 是异面直线,
是异面直线,![]() 是
是![]() ,
,![]() 外的一点,则下列结论中正确的是( )
外的一点,则下列结论中正确的是( )
A.过![]() 有且只有一条直线与
有且只有一条直线与![]() ,
,![]() 都垂直B.过
都垂直B.过![]() 有且只有一条直线与
有且只有一条直线与![]() ,
,![]() 都平行
都平行
C.过![]() 有且只有一个平面与
有且只有一个平面与![]() ,
,![]() 都垂直D.过
都垂直D.过![]() 有且只有一个平面与
有且只有一个平面与![]() ,
,![]() 都平行
都平行
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥![]() 中,底面
中,底面![]() 是平行四边形,
是平行四边形,![]() ,侧面
,侧面![]() 底面
底面![]() ,
,![]() ,
,![]()
![]()
![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,过
的中点,过![]() 的平面与面
的平面与面![]() 交于
交于![]() ,
,![]() 两点.
两点.
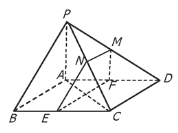
(1)求证:![]() ;
;
(2)求证:平面![]() 平面
平面![]() ;
;
(3)设![]() ,当
,当![]() 为何值时四棱锥
为何值时四棱锥![]() 的体积等于
的体积等于![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知A(﹣2![]() ,0),B
,0),B![]() ,M(x,y)是曲线C上的动点,且直线AM与BM的斜率之积等于
,M(x,y)是曲线C上的动点,且直线AM与BM的斜率之积等于![]() .
.
(1)求曲线C方程;
(2)过D(2,0)的直线l(l与x轴不垂直)与曲线C交于E,F两点,点F关于x轴的对称点为F′,直线EF′与x轴交于点P,求△PEF的面积的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com