
科目:高中数学 来源:2015-2016学年贵州遵义一中高一下第二次联考数学试卷(解析版) 题型:解答题
如图所示,某旅游景点有一座风景秀丽的山峰,山上有一条笔直的山路 和一条索道
和一条索道 ,小王和小李打算不坐索道,而是花2个小时的时间进行徒步攀登,已知
,小王和小李打算不坐索道,而是花2个小时的时间进行徒步攀登,已知 ,
, ,
, (千米),
(千米), (千米). 假设小王和小李徒步攀登的速度为每小时1250米,请问:两位登山爱好者能否在2个小时徒步登上山峰.
(千米). 假设小王和小李徒步攀登的速度为每小时1250米,请问:两位登山爱好者能否在2个小时徒步登上山峰.

查看答案和解析>>
科目:高中数学 来源:2015-2016学年贵州遵义一中高一下第二次联考数学试卷(解析版) 题型:选择题
已知等差数列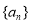 中,前
中,前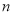 项和
项和 ,若
,若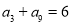 ,则
,则 ( )
( )
A.12 B.33 C.66 D.99
查看答案和解析>>
科目:高中数学 来源:2016届山西省榆林市高三二模理科数学试卷(解析版) 题型:解答题
已知函数 ,(
,( 且
且 ).
).
(1)当 时,若已知
时,若已知 是函数
是函数 的两个极值点,且满足:
的两个极值点,且满足: ,求证:
,求证: ;
;
(2)当 时,①求实数
时,①求实数 的最小值;②对于任意正实数
的最小值;②对于任意正实数 ,当
,当 时,求证:
时,求证: .
.
查看答案和解析>>
科目:高中数学 来源:2016届山西省榆林市高三二模理科数学试卷(解析版) 题型:选择题
过圆 的圆心,作直线分别交
的圆心,作直线分别交 轴、
轴、 轴的正半轴于
轴的正半轴于 、
、 两点,
两点, 被圆分成四部分(如图),若这四部分图形的面积满足
被圆分成四部分(如图),若这四部分图形的面积满足 ,则直线
,则直线 有( )
有( )

A.1条 B.2条 C.3条 D.0条
查看答案和解析>>
科目:高中数学 来源:2016届山西省榆林市高三二模理科数学试卷(解析版) 题型:选择题
已知等比数列 各项都为正数,且
各项都为正数,且 为
为 与
与 的等差中项,则
的等差中项,则 ( )
( )
A.27 B.21 C.14 D.以上都不对
查看答案和解析>>
科目:高中数学 来源:2016届吉林省高三五模文科数学试卷(解析版) 题型:选择题
公元263年左右,我国数学家刘徽发现当圆内接正多边形的边数无限增加时,正多边形的面积可无限逼近于圆的面积,并创立了割圆术,即所谓“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣”。利用割圆术刘徽得到了圆周率精确到小数点后面两位的近似值3.14 ,这就是著名的徽率,利用刘徽的割圆术设计的程序框图,如图所示,则输出的 ( )
( )
(参考数据: )
)

A.24 B.48 C.96 D.192
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com