
分析 (1)证明函数不是奇函数,只要找出关于原点对称的两个点的函数值不等即可;
(2)由奇函数的定义,f(x)+f(-x)=0,代入进行化简,对x∈R恒成立即可得出m,n的值;
(3)由(2)可知f(x)的关系式,由f(x)在R上是单调减函数,且函数y=f(x)为奇函数且,由f(f(x))+f($\frac{1}{9}$)<0,得$f(x)>-\frac{1}{9}$,即可解得不等式.
解答 解:(1)∵当m=n=1时,$f(x)=\frac{{-{3^x}+1}}{{{3^{x+1}}+1}}$,$f(-1)=\frac{1}{3},f(1)=-\frac{1}{5},f(-1)≠f(1)$,
∴函数y=f(x)不是奇函数.…(4分)
(2)由定义,在R上的函数$f(x)=\frac{{-{3^x}+m}}{{{3^{x+1}}+n}}$是奇函数对一切x∈R,f(x)+f(-x)=0恒成立,
即$\frac{-{3}^{x}+m}{{3}^{x+1}+n}$+$\frac{-{3}^{-x}+m}{{3}^{-x+1}+n}$=0,
整理得(3m-n)(3x)2+(2mn-6)3x+3m-n=0对任意x∈R恒成立,
故$\left\{{\begin{array}{l}{3m-n=0}\\{mn=3}\end{array}}\right.$,
解得$\left\{{\begin{array}{l}{m=1}\\{n=3}\end{array}}\right.$,…(10分)
(3)由$f(x)=\frac{1}{3}•\frac{{1-{3^x}}}{{1+{3^x}}}=\frac{1}{3}(\frac{2}{{1+{3^x}}}-1)$在R上是单调减函数,…(12分)
又∵函数y=f(x)为奇函数且,由$f(f(x))+f(\frac{1}{9})<0$得$f(f(x))<f(-\frac{1}{9})$,
∴$f(x)>-\frac{1}{9}$,…(14分)
化简得3x<2,
∴x<log32. …(16分)
点评 本题考查函数的奇偶性的判断,函数奇偶性的定义,考查学生的计算能力和灵活转化问题的能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{7}{24}$ | B. | $-\frac{7}{24}$ | C. | $\frac{24}{7}$ | D. | $-\frac{24}{7}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
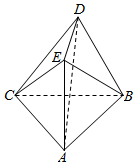 如图,空间几何体ABCDE中,平面ABC⊥平面BCD,AE⊥平面ABC.
如图,空间几何体ABCDE中,平面ABC⊥平面BCD,AE⊥平面ABC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com