
【题目】已知函数![]() 的定义域为
的定义域为![]() ;
;
(1)求实数![]() 的取值范围;
的取值范围;
(2)设实数![]() 为
为![]() 的最大值,若实数
的最大值,若实数![]() ,
,![]() ,
,![]() 满足
满足![]() ,求
,求![]() 的最小值.
的最小值.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)由定义域为R,只需求解|x﹣3|+|x|的最小值,即可得实数m的取值范围(2)根据(1)实数t的值,利用柯西不等式即可求解最小值.
(1)函数![]() 的定义域为R,
的定义域为R,
那么|x﹣3|+|x|﹣m≥0对任意x恒成立,∴只需m≤(|x﹣3|+|x|)min,
根据绝对值不等式|x﹣3|+|﹣x|≥|x﹣3﹣x|=3
∴3﹣m≥0,所以m≤3,
故实数m的取值范围(﹣∞,3];
(2)由(1)可知m的最大值为3,即t=3,
那么a2+b2+c2=t2=9,
则a2+1+b2+1+c2+1=12,
由柯西不等式可得(![]() )(a2+1+b2+1+c2+1)≥(1+1+1)2=9,
)(a2+1+b2+1+c2+1)≥(1+1+1)2=9,
∴(![]() )
)![]() ,当a=b=c
,当a=b=c![]() 时取等号,
时取等号,
故得![]() 的最小值为
的最小值为![]() .
.


科目:高中数学 来源: 题型:
【题目】如图所示,![]() 为山脚两侧共线的3点,在山顶
为山脚两侧共线的3点,在山顶![]() 处测得3点的俯角分别为
处测得3点的俯角分别为![]() ,计划沿直线
,计划沿直线![]() 开通穿山隧道,为求出隧道
开通穿山隧道,为求出隧道![]() 的长度,你认为还需要直接测量出
的长度,你认为还需要直接测量出![]() 中哪些线段的长度?根据条件,并把你认为需要测量的线段长度作为已知量,写出计算隧道
中哪些线段的长度?根据条件,并把你认为需要测量的线段长度作为已知量,写出计算隧道![]() 长度的运算步骤.
长度的运算步骤.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】判断下列结论是否正确(正确的在括号内打“√”,错误的打“×”),并说明理由.
(1)若![]() 与
与![]() 都是单位向量,则
都是单位向量,则![]() .( )
.( )
(2)方向为南偏西60°的向量与北偏东60°的向量是共线向量.( )
(3)直角坐标平面上的x轴、y轴都是向量.( )
(4)若![]() 与
与![]() 是平行向量,则
是平行向量,则![]() .( )
.( )
(5)若用有向线段表示的向量![]() 与
与![]() 不相等,则点M与N不重合.( )
不相等,则点M与N不重合.( )
(6)海拔、温度、角度都不是向量.( )
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知空间几何体![]() 中,
中,![]() 与
与![]() 均为边长为2的等边三角形,
均为边长为2的等边三角形,![]() 为腰长为3的等腰三角形,平面
为腰长为3的等腰三角形,平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() 分别为
分别为![]() 的中点.
的中点.
(1)求证:平面![]() 平面
平面![]() ;
;
(2)求三棱锥![]() 的体积.
的体积.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某渔船在航行中不幸遇险,发出呼叫信号,我海军舰艇在![]() 处获悉后,立即测出该渔船在方位角(从指北方向顺时针转到目标方向线的水平角)为
处获悉后,立即测出该渔船在方位角(从指北方向顺时针转到目标方向线的水平角)为![]() ,距离为15海里的
,距离为15海里的![]() 处,并测得渔船正沿方位角为
处,并测得渔船正沿方位角为![]() 的方向,以15海里/小时的速度向小岛
的方向,以15海里/小时的速度向小岛![]() 靠拢,我海军舰艇立即以
靠拢,我海军舰艇立即以![]() 海里/小时的速度前去营救,求舰艇靠近渔船所需的最少时间和舰艇的航向.
海里/小时的速度前去营救,求舰艇靠近渔船所需的最少时间和舰艇的航向.
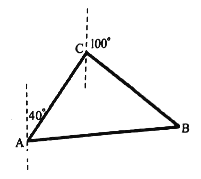
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】通过随机询问![]() 名不同性别的大学生在购买食物时是否看营养说明,得到如下列联表:
名不同性别的大学生在购买食物时是否看营养说明,得到如下列联表:
男 | 女 | 总计 | |
读营养说明 |
|
|
|
不读营养说明 |
|
|
|
总计 |
|
|
|
附:
|
|
|
|
|
|
|
|
![]()
(1)由以上列联表判断,能否在犯错误的概率不超过![]() 的前提下认为性别和是否看营养说明有关系呢?
的前提下认为性别和是否看营养说明有关系呢?
(2)从被询问的![]() 名不读营养说明的大学生中随机选取
名不读营养说明的大学生中随机选取![]() 名学生,求抽到女生人数
名学生,求抽到女生人数![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com