
【题目】已知抛物线![]() :
:![]() ,
,![]() ,
,![]() 是抛物线
是抛物线![]() 上的两点,
上的两点,![]() 是坐标原点,且
是坐标原点,且![]() .
.
(1)若![]() ,求
,求![]() 的面积;
的面积;
(2)设![]() 是线段
是线段![]() 上一点,若
上一点,若![]() 与
与![]() 的面积相等,求
的面积相等,求![]() 的轨迹方程.
的轨迹方程.
【答案】(1)16(2) ![]()
【解析】
分析:(1)![]() ,由抛物线的对称性可知
,由抛物线的对称性可知![]() ,
,![]() 关于
关于![]() 轴对称设出点的关系;
轴对称设出点的关系;![]() ,求出
,求出![]() ,
,![]() 点的坐标,求出面积。
点的坐标,求出面积。
![]() 与
与![]() 的面积相等,所以
的面积相等,所以![]() 为
为![]() 的中点,利用消参法求出轨迹方程
的中点,利用消参法求出轨迹方程
详解:设![]() ,
,![]() ,
,
(1)因为![]() ,
,
又由抛物线的对称性可知![]() ,
,![]() 关于
关于![]() 轴对称,
轴对称,
所以![]() ,
,![]() ,
,
因为![]() ,所以
,所以![]() ,故
,故![]() ,
,
则![]() ,又
,又![]() ,
,
解得![]() 或
或![]() (舍),
(舍),
所以![]() ,于是
,于是![]() 的面积为
的面积为![]() .
.
(2)直线![]() 的斜率存在,设直线
的斜率存在,设直线![]() 的方程为
的方程为![]() ,
,
代入![]() ,得
,得![]() ,
,![]() ,
,
且![]() ,
,![]() ,
,
因为![]() ,所以
,所以![]() ,
,
故![]() ,则
,则![]() ,
,
所以![]() 或
或![]() (舍),
(舍),
因为![]() 与
与![]() 的面积相等,所以
的面积相等,所以![]() 为
为![]() 的中点,
的中点,
则![]() 点的横坐标为
点的横坐标为![]() ,纵坐标为
,纵坐标为![]() ,
,
故![]() 点的轨迹方程为
点的轨迹方程为![]() .
.
点晴:圆锥曲线类的题目,画出相应的草图,对题目给出的关键信息进行分析转化是做题的要点,然后选取相应的方法进行解决问题,计算量较大,计算的过程中含参的较多,大家要做到多想少算。


科目:高中数学 来源: 题型:
【题目】某学校为了分析在一次数学竞赛中甲、乙两个班的数学成绩,分别从甲、乙两个班中随机抽取了10个学生的成绩,成绩的茎叶图如下:
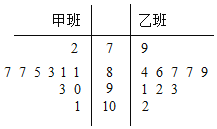
(Ⅰ)根据茎叶图,计算甲班被抽取学生成绩的平均值![]() 及方差
及方差![]() ;
;
(Ⅱ)若规定成绩不低于90分的等级为优秀,现从甲、乙两个班级所抽取成绩等级为优秀的学生中,随机抽取2人,求这两个人恰好都来自甲班的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知一定点![]() ,及一定直线
,及一定直线![]() :
:![]() ,以动点
,以动点![]() 为圆心的圆
为圆心的圆![]() 过点
过点![]() ,且与直线
,且与直线![]() 相切.
相切.
(Ⅰ)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(Ⅱ)设![]() 在直线
在直线![]() 上,直线
上,直线![]() ,
,![]() 分别与曲线
分别与曲线![]() 相切于
相切于![]() ,
,![]() ,
,![]() 为线段
为线段![]() 的中点.求证:
的中点.求证:![]() ,且直线
,且直线![]() 恒过定点.
恒过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量![]() ,
,![]() ,设函数
,设函数![]() .
.
(1)若函数![]() 的图象关于直线
的图象关于直线![]() 对称,且
对称,且![]() 时,求函数
时,求函数![]() 的单调增区间;
的单调增区间;
(2)在(1)的条件下,当![]() 时,函数
时,函数![]() 有且只有一个零点,求实数
有且只有一个零点,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com