
【题目】已知函数![]() 的定义域为
的定义域为![]() ;
;
(1)求实数![]() 的取值范围;
的取值范围;
(2)设实数![]() 为
为![]() 的最大值,若实数
的最大值,若实数![]() ,
,![]() ,
,![]() 满足
满足![]() ,求
,求![]() 的最小值.
的最小值.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)由定义域为R,只需求解|x﹣3|+|x|的最小值,即可得实数m的取值范围(2)根据(1)实数t的值,利用柯西不等式即可求解最小值.
(1)函数![]() 的定义域为R,
的定义域为R,
那么|x﹣3|+|x|﹣m≥0对任意x恒成立,∴只需m≤(|x﹣3|+|x|)min,
根据绝对值不等式|x﹣3|+|﹣x|≥|x﹣3﹣x|=3
∴3﹣m≥0,所以m≤3,
故实数m的取值范围(﹣∞,3];
(2)由(1)可知m的最大值为3,即t=3,
那么a2+b2+c2=t2=9,
则a2+1+b2+1+c2+1=12,
由柯西不等式可得(![]() )(a2+1+b2+1+c2+1)≥(1+1+1)2=9,
)(a2+1+b2+1+c2+1)≥(1+1+1)2=9,
∴(![]() )
)![]() ,当a=b=c
,当a=b=c![]() 时取等号,
时取等号,
故得![]() 的最小值为
的最小值为![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
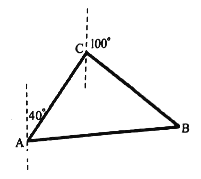
【题目】某渔船在航行中不幸遇险,发出呼叫信号,我海军舰艇在![]() 处获悉后,立即测出该渔船在方位角(从指北方向顺时针转到目标方向线的水平角)为
处获悉后,立即测出该渔船在方位角(从指北方向顺时针转到目标方向线的水平角)为![]() ,距离为15海里的
,距离为15海里的![]() 处,并测得渔船正沿方位角为
处,并测得渔船正沿方位角为![]() 的方向,以15海里/小时的速度向小岛
的方向,以15海里/小时的速度向小岛![]() 靠拢,我海军舰艇立即以
靠拢,我海军舰艇立即以![]() 海里/小时的速度前去营救,求舰艇靠近渔船所需的最少时间和舰艇的航向.
海里/小时的速度前去营救,求舰艇靠近渔船所需的最少时间和舰艇的航向.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的一个焦点为
的一个焦点为![]() ,离心率为
,离心率为![]() .不过原点的直线
.不过原点的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点,设直线
两点,设直线![]() ,直线
,直线![]() ,直线
,直线![]() 的斜率分别为
的斜率分别为![]() ,且
,且![]() 成等比数列.
成等比数列.
(1)求![]() 的值;
的值;
(2)若点![]() 在椭圆
在椭圆![]() 上,满足
上,满足![]() 的直线
的直线![]() 是否存在?若存在,求出直线
是否存在?若存在,求出直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】判断下列命题的真假.
(1)过一条直线的平面有无数多个;
(2)如果两个平面有两个公共点![]() ,那么它们就有无数多个公共点,并且这些公共点都在直线
,那么它们就有无数多个公共点,并且这些公共点都在直线![]() 上;
上;
(3)两个平面的公共点组成的集合,可能是一条线段;
(4)两个相交平面可能存在不在一条直线上的3个公共点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】通过随机询问![]() 名不同性别的大学生在购买食物时是否看营养说明,得到如下列联表:
名不同性别的大学生在购买食物时是否看营养说明,得到如下列联表:
男 | 女 | 总计 | |
读营养说明 |
|
|
|
不读营养说明 |
|
|
|
总计 |
|
|
|
附:
|
|
|
|
|
|
|
|
![]()
(1)由以上列联表判断,能否在犯错误的概率不超过![]() 的前提下认为性别和是否看营养说明有关系呢?
的前提下认为性别和是否看营养说明有关系呢?
(2)从被询问的![]() 名不读营养说明的大学生中随机选取
名不读营养说明的大学生中随机选取![]() 名学生,求抽到女生人数
名学生,求抽到女生人数![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,某铁制零件由一个正四棱柱和一个球组成,已知正四棱柱底面边长与球的直径均为1cm,正四棱柱的高为2cm.现有这种零件一盒共50kg,取铁的密度为![]() ,
,![]() .
.
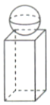
(1)估计有多少个这样的零件;
(2)如果要给这盒零件的每个零件表面涂上一种特殊的材料,则需要能涂多少平方厘米的材料(球与棱柱接口处的面积不计,结果精确到![]() )?
)?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com