
【题目】F是抛物线![]() 的焦点,M是抛物线C上位于第一象限内的任意一点,过
的焦点,M是抛物线C上位于第一象限内的任意一点,过![]() 三点的圆的圆心为Q,点Q到抛物线C的准线的距离为
三点的圆的圆心为Q,点Q到抛物线C的准线的距离为![]() .
.
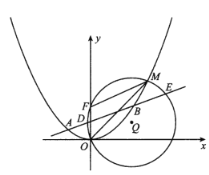
(1)求抛物线C的方程;
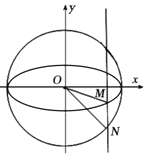
(2)若点M的横坐标为![]() ,直线
,直线![]() 与抛物线C有两个不同的交点A,B,l与圆Q有两个不同的交点D,E,求当
与抛物线C有两个不同的交点A,B,l与圆Q有两个不同的交点D,E,求当![]() 时,
时,![]() 的最小值.
的最小值.
科目:高中数学 来源: 题型:
【题目】在等比数列![]() 中,已知
中,已知![]() 设数列
设数列![]() 的前n项和为
的前n项和为![]() ,且
,且![]()
(1)求数列![]() 通项公式;
通项公式;
(2)证明:数列![]() 是等差数列;
是等差数列;
(3)是否存在等差数列![]() ,使得对任意
,使得对任意![]() ,都有
,都有![]() ?若存在,求出所有符合题意的等差数列
?若存在,求出所有符合题意的等差数列![]() ;若不存在,请说明理由.
;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,定义:以椭圆中心为圆心,长轴为直径的圆叫做椭圆的“辅助圆”.过椭圆第四象限内一点M作x轴的垂线交其“辅助圆”于点N,当点N在点M的下方时,称点N为点M的“下辅助点”.已知椭圆![]() 上的点
上的点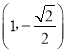 的下辅助点为(1,﹣1).
的下辅助点为(1,﹣1).
(1)求椭圆E的方程;
(2)若△OMN的面积等于![]() ,求下辅助点N的坐标;
,求下辅助点N的坐标;
(3)已知直线l:x﹣my﹣t=0与椭圆E交于不同的A,B两点,若椭圆E上存在点P,使得四边形OAPB是对边平行且相等的四边形.求直线l与坐标轴围成的三角形面积最小时的m2+t2的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】直线l:x﹣y![]() 0将圆O:
0将圆O:![]() 分成的两部分的面积之比为( )
分成的两部分的面积之比为( )
A.(4π![]() ):(8π
):(8π![]() )B.(4π﹣3
)B.(4π﹣3![]() ):(8π+3
):(8π+3![]() )
)
C.(2π﹣2![]() ):(10π+2
):(10π+2![]() )D.(2π﹣3
)D.(2π﹣3![]() ):(10π+3
):(10π+3![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 年上半年,随着新冠肺炎疫情在全球蔓延,全球超过
年上半年,随着新冠肺炎疫情在全球蔓延,全球超过![]() 个国家或地区宣布进人紧急状态,部分国家或地区直接宣布“封国”或“封城”,随着国外部分活动进入停摆,全球经济缺乏活力,一些企业开始倒闭,下表为
个国家或地区宣布进人紧急状态,部分国家或地区直接宣布“封国”或“封城”,随着国外部分活动进入停摆,全球经济缺乏活力,一些企业开始倒闭,下表为![]() 年第一季度企业成立年限与倒闭分布情况统计表:
年第一季度企业成立年限与倒闭分布情况统计表:
企业成立年份 | 2019 | 2018 | 2017 | 2016 | 2015 |
企业成立年限 | 1 | 2 | 3 | 4 | 5 |
倒闭企业数量(万家) | 5.28 | 4.72 | 3.58 | 2.70 | 2.15 |
倒闭企业所占比例 | 21.4% | 19.1% | 14.5% | 10.9% | 8.7% |
(1)由所给数据可用线性回归模型拟合![]() 与
与![]() 的关系,请用相关系数加以说明;
的关系,请用相关系数加以说明;
(2)建立![]() 关于
关于![]() 的回归方程,预测
的回归方程,预测![]() 年成立的企业中倒闭企业所占比例.
年成立的企业中倒闭企业所占比例.
参考数据:![]() ,
,![]() ,
,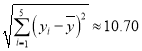 ,
,![]() ,
,
相关系数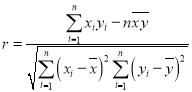 ,样本
,样本![]() 的最小二乘估计公式为
的最小二乘估计公式为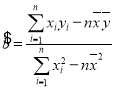 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 满足
满足![]() ,
,![]() ,其中常数
,其中常数![]() .
.
(Ⅰ)若![]() ,求
,求![]() 的取值范围;
的取值范围;
(Ⅱ)若![]() ,求证:对于任意的
,求证:对于任意的![]() ,均有
,均有![]() ;
;
(Ⅲ)当常数![]() 时,设
时,设![]() ,若存在实数
,若存在实数![]() 使得
使得![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】依法纳税是公民应尽的义务,随着经济的发展,个人收入的提高,自2018年10月1日起,个人所得税起征点和税率进行了调整,调整前后的计算方法如下表,2018年12月22日国务院又印发了《个人所得税专项附加扣除暂行办法》(以下简称《办法》),自2019年1月1日起施行,该《办法》指出,个人所得税专项附加扣除,是指个人所得税法规定的子女教育、继续教育、大病医疗、住房贷款利息或者住房租金、赡养老人等6项专项附加扣除.简单来说,2018年10月1日之前,“应纳税所得额”![]() “税前收入”
“税前收入”![]() “险金”
“险金”![]() “基本减除费用(统一为3500元)”
“基本减除费用(统一为3500元)”![]() “依法扣除的其他扣除费用”;自2019年1月1日起,“应纳税所得额”
“依法扣除的其他扣除费用”;自2019年1月1日起,“应纳税所得额”![]() “税前收人”
“税前收人”![]() “险金”
“险金”![]() “基本减除费用(统一为5000元)”
“基本减除费用(统一为5000元)”![]() “专项附加扣除费用”
“专项附加扣除费用”![]() “依法扣除的其他扣除费用.
“依法扣除的其他扣除费用.
调整前后个人所得税税率表如下:
个人所得税税率表(调整前) | 个人所得税税率表(调整后) | ||||
级数 | 全月应纳税所得额 | 税率(%) | 级数 | 全月应纳税所得额 | 税率(%) |
1 | 不超过1500元的部分 | 3 | 1 | 不超过3000元的部分 | 3 |
2 | 超过1500元至4500元的部分 | 10 | 2 | 超过3000元至12000元的部分 | 10 |
3 | 超过4500元至9000元的部分 | 20 | 3 | 超过12000元至25000元的部分 | 20 |
… | … | … | … | … | … |
某税务部门在小李所在公司利用分层抽样方法抽取某月100个不同层次员工的税前收入,扣除险金后,制成下面的频数分布表:
收入(元) |
|
|
|
|
|
|
人数 | 10 | 20 | 25 | 20 | 15 | 10 |
(Ⅰ)估算小李公司员工该月扣除险金后的平均收入为多少?
(Ⅱ)若小李在该月扣除险金后的收入为10000元,假设小李除住房租金一项专项扣除费用1500元外,无其他依法扣除费用,则2019年1月1日起小李的个人所得税,比2018年10月1日之前少交多少?
(Ⅲ)先从收入在[9000,11000)及[11000,13000)的人群中按分层抽样抽取7人,再从中选2人作为新纳税法知识宜讲员,求两个宣讲员不全是同一收入人群的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
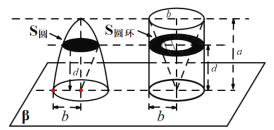
【题目】我国南北朝时期的数学家祖暅提出了一条原理:“幂势既同,则积不容异”即夹在两个平行平面之间的两个几何体,被平行于这两个平面的任意平面所截,如果截得的两个截面的面积总相等,那么这两个几何体的体积相等.椭球是椭圆绕其长轴旋转所成的旋转体,如图,将底面半径都为![]() .高都为
.高都为![]() 的半椭球和已被挖去了圆锥的圆柱(被挖去的圆锥以圆柱的上底面为底面,下底面的圆心为顶点)放置于同一平面
的半椭球和已被挖去了圆锥的圆柱(被挖去的圆锥以圆柱的上底面为底面,下底面的圆心为顶点)放置于同一平面![]() 上,用平行于平面
上,用平行于平面![]() 且与平面
且与平面![]() 任意距离
任意距离![]() 处的平面截这两个几何体,截面分别为圆面和圆环,可以证明
处的平面截这两个几何体,截面分别为圆面和圆环,可以证明![]() 圆=
圆=![]() 圆环总成立.据此,椭圆的短半轴长为2,长半轴长为4的椭球的体积是( )
圆环总成立.据此,椭圆的短半轴长为2,长半轴长为4的椭球的体积是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com