
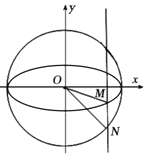
����Ŀ����ͼ�����壺����Բ����ΪԲ�ģ�����Ϊֱ����Բ������Բ�ġ�����Բ��������Բ����������һ��M��x��Ĵ��߽��䡰����Բ���ڵ�N������N�ڵ�M���·�ʱ���Ƶ�NΪ��M�ġ��¸����㡱����֪��Բ![]() �ϵĵ�
�ϵĵ�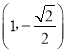 ���¸�����Ϊ��1����1����
���¸�����Ϊ��1����1����
��1������ԲE�ķ��̣�
��2������OMN���������![]() �����¸�����N�����ꣻ
�����¸�����N�����ꣻ
��3����ֱ֪��l��x��my��t��0����ԲE���ڲ�ͬ��A��B���㣬����ԲE�ϴ��ڵ�P��ʹ���ı���OAPB�ǶԱ�ƽ������ȵ��ı��Σ���ֱ��l��������Χ�ɵ������������Сʱ��m2+t2��ֵ��
���𰸡���1��![]() y2��1����2����
y2��1����2����![]() ��
��![]() �� ��
�� ��![]() ��
��![]() ������3��3��
������3��3��
��������
��1������Բ���ĵ���������Բx2+y2��a2�������꣬����ɵ�a��b��ֵ�����������Բ�ķ��̣�
��2����N�������M�����꣬������Բ����Բ���N��M������Ĺ�ϵ�����������OMN�����S��OMN![]() x0��y1��y0��
x0��y1��y0��![]() ����x0y1
����x0y1![]() �ͣ�
�ͣ�![]() y12��1����������¸�����N�����ꣻ
y12��1����������¸�����N�����ꣻ
��3����A��B�����꽫ֱ��AB�ķ�������Բ�����������֮�ͼ�����֮�������AB���е����꣬��Ϊ�ı���OAPB�ǶԱ�ƽ������ȣ����ı���OAPBǡ��Ϊƽ���ı��Σ�����![]() ������������OAB���Ϊ
������������OAB���Ϊ �����ҽ���m2��2��t2��1ʱȡ�Ⱥţ������ɵ�m2+t2��ֵΪ3��
�����ҽ���m2��2��t2��1ʱȡ�Ⱥţ������ɵ�m2+t2��ֵΪ3��
��1����Ϊ��ԲE��![]() 1�����㣨1��
1�����㣨1��![]() ��������Բx2+y2��a2����1��1�������Կɵ�a2��12+����1��2��2��
��������Բx2+y2��a2����1��1�������Կɵ�a2��12+����1��2��2��
������Բ��ʵ���᳤��ƽ��a2��2��
����![]() 1����ã�b2��1��
1����ã�b2��1��
����ԲE�ķ���Ϊ��![]() y2��1��
y2��1��
��2�����N��x0��y0������y0��0������������ɵõ�M��x0��y1������y1��0��������������ֱ���븨��Բ���̺���Բ���̿ɵã�x02+y02��2��![]() y12��1��
y12��1��
��y02��2y12����y0![]() ��
��
��S��OMN![]() x0��y1��y0��
x0��y1��y0��![]() ����x0y1
����x0y1![]()
���� ���ɽ��
���ɽ�� ��
�� �����¸�����N ������Ϊ��
�����¸�����N ������Ϊ��![]() ��
��![]() �� ��
�� ��![]() ��
��![]() ����
����
��3�����������A��x1��y1����B��x2��y2����
���� �����ã�m2+2��y2+2mty+t2��2��0��
�����ã�m2+2��y2+2mty+t2��2��0��
�����8��m2+2��t2����0��
����Τ�ﶨ���� ��
��
��Ϊ�ı���OAPB�ǶԱ�ƽ������ȣ����ı���OAPBǡ��Ϊƽ���ı��Σ�
����![]() ������
������![]() ��
��![]()
��Ϊ��P����ԲE �ϣ�����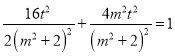 ��
��
������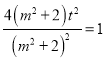 ����4t2��m2+2��
����4t2��m2+2��
��ֱ��l��x��my��t��0�У�����ֱ��l��������Χ�������Σ���t��0��m��0��
��x��0����![]() ����y��0����x��t��
����y��0����x��t��
����������OAB���Ϊ ��
��
���ҽ���m2��2��t2��1ʱ��ȡ�Ⱥţ���ʱ����24��0������m2+t2��3��
������m2+t2 ��ֵΪ3��


 ��ѧʵ����ϵ�д�
��ѧʵ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����й�ʣ�ඨ�����ֳơ����Ӷ�����������ɼ����й��ϱ���ʱ�ڵ���ѧ�����������㾭�����µڶ�ʮ���⣬�������ﲻ֪������ԭ�����£������ﲻ֪������������֮ʣ����������֮ʣ����������֮ʣ�������X�Σ���������һ����ص����⣺��1��2020��2020����Ȼ�������㱻3����2�ұ�5����3�������մ�С�����˳���ų�һ�У�����һ�����У�������е������ǣ� ��
A.135B.134C.59D.58
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڡ�ABC�У����ڽ�A��B��C����![]() ��
��
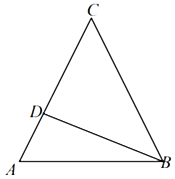
�����жϡ�ABC����״��
��������D���߶�AC�ϣ���CD��2DA��![]() ����tanA��ֵ��
����tanA��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������ҹ�����ȡ���˳���Ľ�����ͬʱ�Ա������������ͻ��.���ݹ���ͳ�ƾַ�����2019��ͳ�������������31��ʡ�����������ر�������δ���ˣ����˾�����������ֵ���˿��Ա������ÿ100λŮ������Ӧ��������Ŀ��������������״ͼ.���˿�ͳ��ѧ�Ƕ���˵���Ա����������Χ��102��107֮��.�˾�����������ֵС��6.5��Ԫ����ң�Լ1����Ԫ����ΪǷ������������ڻ����6.5��Ԫ�ĵ�����Ϊ�������.
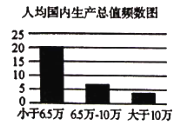
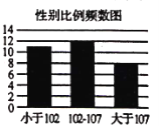
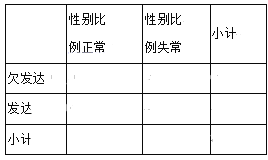
��1����֪�Ա����������ʡ����������Ƿ������������ĸ����Ƿ�������������������������������ж��Ƿ���90%�İ�����Ϊ��ʡ�����������Ա�����뾭�÷�չ�̶��йأ�
��2�����˾�����������ֵ����6.5����10��֮���7ʡ���������У���3���˿��Ա����������������ȡ��������鵽����ʡ�����������˿��Ա�����������ĸ���.
�����ο���ʽ���ٽ�ֵ��
 ��
��![]()
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��������ABC��A1B1C1�ĵ���߳�Ϊ![]() ���Ҹ������������ı����Ϊ14������PΪ����A1B1C1�����ģ���PA��ƽ��ABC���ɽǵĴ�СΪ�� ��
���Ҹ������������ı����Ϊ14������PΪ����A1B1C1�����ģ���PA��ƽ��ABC���ɽǵĴ�СΪ�� ��
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ԲC��![]() ��a��b��0�����ҽ���ΪF����ԲC�ϵ�����A��B����ԭ��Գƣ�������
��a��b��0�����ҽ���ΪF����ԲC�ϵ�����A��B����ԭ��Գƣ�������![]() ��|FB|��|FA|��2|FB|������ԲC�������ʵ�ȡֵ��Χ�ǣ� ��
��|FB|��|FA|��2|FB|������ԲC�������ʵ�ȡֵ��Χ�ǣ� ��
A. B.
B.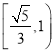
C.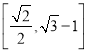 D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪����![]() ��
��![]() �ǵȱ������Σ�
�ǵȱ������Σ�![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ���е㣮
���е㣮
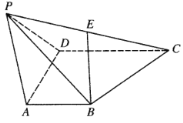
������֤����ֱ��![]() ƽ��
ƽ��![]() ��
��
��������ֱ��![]() ��ƽ��
��ƽ��![]() ���ɽǵ�����ֵ��
���ɽǵ�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��F��������![]() �Ľ��㣬M��������C��λ�ڵ�һ�����ڵ�����һ�㣬��
�Ľ��㣬M��������C��λ�ڵ�һ�����ڵ�����һ�㣬��![]() �����Բ��Բ��ΪQ����Q��������C���ߵľ���Ϊ
�����Բ��Բ��ΪQ����Q��������C���ߵľ���Ϊ![]() .
.
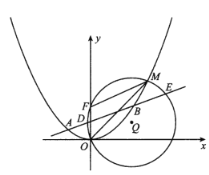
��1����������C�ķ��̣�
��2������M�ĺ�����Ϊ![]() ��ֱ��
��ֱ��![]() ��������C��������ͬ�Ľ���A��B��l��ԲQ��������ͬ�Ľ���D��E����
��������C��������ͬ�Ľ���A��B��l��ԲQ��������ͬ�Ľ���D��E����![]() ʱ��
ʱ��![]() ����Сֵ.
����Сֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ![]() �У�ֱ��
�У�ֱ��![]() �IJ�������Ϊ
�IJ�������Ϊ![]() ������
������![]() ��������
��������![]() ������
������![]() Ϊ���㡢
Ϊ���㡢![]() ��ķǸ�����Ϊ����ļ�����ϵ����������ϵȡ��ͬ�ĵ�λ���ȣ��У�����
��ķǸ�����Ϊ����ļ�����ϵ����������ϵȡ��ͬ�ĵ�λ���ȣ��У�����![]() �ļ����귽��Ϊ
�ļ����귽��Ϊ![]() ����ֱ��
����ֱ��![]() ��������
��������![]() ����������
����������![]() ����
����![]() ��
��![]() ���㣮
���㣮
�������![]() ��ֱ�����꼰����
��ֱ�����꼰����![]() ��ֱ�����귽�̣�
��ֱ�����귽�̣�
������֤������![]() Ϊ��ֵʱ��
Ϊ��ֵʱ��![]() Ϊ��ֵ��
Ϊ��ֵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com