
【题目】在△ABC中,三内角A,B,C满足![]() .
.
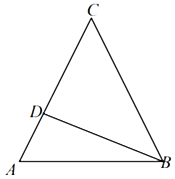
(Ⅰ)判断△ABC的形状;
(Ⅱ)若点D在线段AC上,且CD=2DA,![]() ,求tanA的值.
,求tanA的值.
【答案】(Ⅰ)△ABC的形状为等腰三角形;(Ⅱ)tanA=2.
【解析】
(Ⅰ)由已知利用三角函数恒等变换的应用化简可得cos(A﹣B)=1,结合范围A﹣B∈(﹣π,π),可得A=B,即可判断△ABC的形状为等腰三角形;
(Ⅱ)设DA=x,CD=2x,∠ABD=θ,在△ADB,△CDB中,由正弦定理可得![]() ,利用三角函数恒等变换的应用可求tanA=5tanθ,结合tanθ
,利用三角函数恒等变换的应用可求tanA=5tanθ,结合tanθ![]() ,可求tanA的值.
,可求tanA的值.
解:(Ⅰ)∵![]() ,
,
∴sinAsinB=1﹣sin2![]() cos2
cos2![]() ,
,
∴2sinAsinB=1+cosC,
∵C=π﹣(A+B),
∴2sinAsinB=1+cos[π﹣(A+B)]=1﹣cos(A+B),
∴2sinAsinB=1﹣cosAcosB+sinAsinB,
即cosAcosB+sinAsinB=1,即cos(A﹣B)=1,
∵A﹣B∈(﹣π,π),
∴A﹣B=0,可得A=B,可得△ABC的形状为等腰三角形;
(Ⅱ)设DA=x,CD=2x,∠ABD=θ,
在△ADB中,由正弦定理可得![]() ,即
,即![]() ,
,
在△CDB中,由正弦定理可得![]() ,
,
即![]() ,即
,即![]() ,
,
∴![]() ,
,
∴sin(A﹣θ)=4cosAsinθ,
∴sinAcosθ﹣cosAsinθ=4cosAsinθ,
∴sinAcosθ=5cosAsinθ,
∴tanA=5tanθ,
∵tanθ![]() ,
,
∴tanA=2.


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案科目:高中数学 来源: 题型:
【题目】国际上通常用年龄中位数指标作为划分国家或地区人口年龄构成的标准:年龄中位数在20岁以下为“年轻型”人口;年龄中位数在20~30岁为“成年型”人口;年龄中位数在30岁以上为“老龄型”人口.

如图反映了我国全面放开二孩政策对我国人口年龄中位数的影响.据此,对我国人口年龄构成的类型做出如下判断:①建国以来直至2000年为“成年型”人口;②从2010年至2020年为“老龄型”人口;③放开二孩政策之后我国仍为“老龄型”人口.其中正确的是( )
A.②③B.①③C.②D.①②
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在等比数列![]() 中,已知
中,已知![]() 设数列
设数列![]() 的前n项和为
的前n项和为![]() ,且
,且![]()
(1)求数列![]() 通项公式;
通项公式;
(2)证明:数列![]() 是等差数列;
是等差数列;
(3)是否存在等差数列![]() ,使得对任意
,使得对任意![]() ,都有
,都有![]() ?若存在,求出所有符合题意的等差数列
?若存在,求出所有符合题意的等差数列![]() ;若不存在,请说明理由.
;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是九江市2019年4月至2020年3月每月最低气温与最高气温(℃)的折线统计图:已知每月最低气温与最高气温的线性相关系数r=0.83,则下列结论错误的是( )
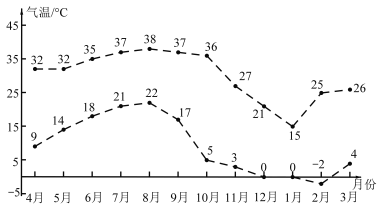
A.每月最低气温与最高气温有较强的线性相关性,且二者为线性正相关
B.月温差(月最高气温﹣月最低气温)的最大值出现在10月
C.9﹣12月的月温差相对于5﹣8月,波动性更大
D.每月最高气温与最低气温的平均值在前6个月逐月增加
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为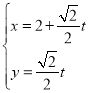 (
(![]() 为参数),曲线
为参数),曲线![]() 的参数方程为
的参数方程为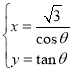 (
(![]() 为参数).
为参数).
(1)求曲线![]() ,
,![]() 的普通方程;
的普通方程;
(2)已知点![]() ,若曲线
,若曲线![]() ,
,![]() 交于
交于![]() ,
,![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,定义:以椭圆中心为圆心,长轴为直径的圆叫做椭圆的“辅助圆”.过椭圆第四象限内一点M作x轴的垂线交其“辅助圆”于点N,当点N在点M的下方时,称点N为点M的“下辅助点”.已知椭圆![]() 上的点
上的点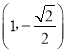 的下辅助点为(1,﹣1).
的下辅助点为(1,﹣1).
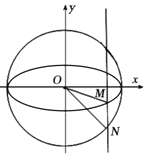
(1)求椭圆E的方程;
(2)若△OMN的面积等于![]() ,求下辅助点N的坐标;
,求下辅助点N的坐标;
(3)已知直线l:x﹣my﹣t=0与椭圆E交于不同的A,B两点,若椭圆E上存在点P,使得四边形OAPB是对边平行且相等的四边形.求直线l与坐标轴围成的三角形面积最小时的m2+t2的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 满足
满足![]() ,
,![]() ,其中常数
,其中常数![]() .
.
(Ⅰ)若![]() ,求
,求![]() 的取值范围;
的取值范围;
(Ⅱ)若![]() ,求证:对于任意的
,求证:对于任意的![]() ,均有
,均有![]() ;
;
(Ⅲ)当常数![]() 时,设
时,设![]() ,若存在实数
,若存在实数![]() 使得
使得![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com