
【题目】国际上通常用年龄中位数指标作为划分国家或地区人口年龄构成的标准:年龄中位数在20岁以下为“年轻型”人口;年龄中位数在20~30岁为“成年型”人口;年龄中位数在30岁以上为“老龄型”人口.

如图反映了我国全面放开二孩政策对我国人口年龄中位数的影响.据此,对我国人口年龄构成的类型做出如下判断:①建国以来直至2000年为“成年型”人口;②从2010年至2020年为“老龄型”人口;③放开二孩政策之后我国仍为“老龄型”人口.其中正确的是( )
A.②③B.①③C.②D.①②
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() 是
是![]() 上的奇函数,其中
上的奇函数,其中![]() ,则下 列关于函数
,则下 列关于函数![]() 的描述中,其中正确的是( )
的描述中,其中正确的是( )
①将函数![]() 的图象向右平移
的图象向右平移![]() 个单位可以得到函数
个单位可以得到函数![]() 的图象;
的图象;
②函数![]() 图象的一条对称轴方程为
图象的一条对称轴方程为![]() ;
;
③当![]() 时,函数
时,函数![]() 的最小值为
的最小值为![]() ;
;
④函数![]() 在
在![]() 上单调递增.
上单调递增.
A.①③B.③④C.②③D.②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“中国剩余定理”又称“孙子定理”,最早可见于中国南北朝时期的数学著作《孙子算经》卷下第二十六题,叫做“物不知数”,原文如下:今有物不知其数,三三数之剩二,五五数之剩三,七七数之剩二,问物几何?现有这样一个相关的问题:将1到2020这2020个自然数中满足被3除余2且被5除余3的数按照从小到大的顺序排成一列,构成一个数列,则该数列的项数是( )
A.135B.134C.59D.58
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】过点![]() 作圆
作圆![]() 的切线
的切线![]() ,已知
,已知![]() ,
,![]() 分别为切点,直线
分别为切点,直线![]() 恰好经过椭圆的右焦点和下顶点,则直线
恰好经过椭圆的右焦点和下顶点,则直线![]() 方程为___________;椭圆的标准方程是__________.
方程为___________;椭圆的标准方程是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】天上有些恒星的亮度是会变化的,其中一种称为造父(型)变星,本身体积会膨胀收缩造成亮度周期性的变化.第一颗被描述的经典造父变星是在1784年.
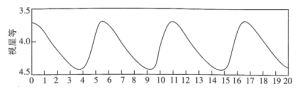
上图为一造父变星的亮度随时间的周期变化图,其中视星等的数值越小,亮度越高,则此变星亮度变化的周期、最亮时视星等,分别约是( )
A.5.5,3.7B.5.4,4.4C.6.5,3.7D.5.5,4.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() .
.
(1)曲线![]() :
:![]() 与
与![]() 相交于
相交于![]() ,
,![]() 两点,
两点,![]() 为
为![]() 上异于
上异于![]() ,
,![]() 的点,若直线
的点,若直线![]() 的斜率为1,求直线
的斜率为1,求直线![]() 的斜率;
的斜率;
(2)若![]() 的左焦点为
的左焦点为![]() ,右顶点为
,右顶点为![]() ,直线
,直线![]() :
:![]() .过
.过![]() 的直线
的直线![]() 与
与![]() 相交于
相交于![]() ,
,![]() (
(![]() 在第一象限)两点,与
在第一象限)两点,与![]() 相交于
相交于![]() ,是否存在
,是否存在![]() 使
使![]() 的面积等于
的面积等于![]() 的面积与
的面积与![]() 的面积之和.若存在,求直线
的面积之和.若存在,求直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com