
【题目】如图,已知四棱锥![]() ,
,![]() 是等边三角形,
是等边三角形,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 的中点.
的中点.
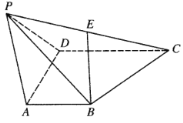
(Ⅰ)证明:直线![]() 平面
平面![]() ;
;
(Ⅱ)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(Ⅰ)证明见解析;(Ⅱ)![]()
【解析】
(Ⅰ)先证明![]() 与平面
与平面![]() 中的一条线平行,再应用线面平行的判定定理即可证得结果;
中的一条线平行,再应用线面平行的判定定理即可证得结果;
(Ⅱ)过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,过点
,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,由此可推出
,由此可推出![]() 为点
为点![]() 到平面
到平面![]() 的距离,然后通过解直角三角形求解即可.
的距离,然后通过解直角三角形求解即可.
(Ⅰ)证明:取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,![]() ,
,
在![]() 中,
中,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点,
的中点,
所以![]() 且
且![]() ,
,
又![]() 且
且![]() ,
,
所以![]() ,且
,且![]() ,
,
所以四边形![]() 为平行四边形,
为平行四边形,
所以![]() ,
,
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
故![]() 平面
平面![]() .
.

(Ⅱ)过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,过点
,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,
,
由![]() ,
,![]() ,
,![]() ,
,
得![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() ,
,
过点![]() 作
作![]() 于点
于点![]() ,则
,则![]() 平面
平面![]() ,
,
由![]() 知,点
知,点![]() 到平面
到平面![]() 的距离等于
的距离等于![]() ,
,
设![]() ,则由
,则由![]() 知
知![]() ,
,![]() ,
,![]() ,
,
又![]() ,所以
,所以![]() 平面
平面![]() ,
,
所以![]() ,
,
又![]() ,
,![]() ,所以
,所以![]() ,
,
所以![]() ,又
,又![]() ,
,
![]() ,则
,则![]() ,
,
![]() ,
,
即![]() ,解得
,解得![]() ,
,
在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
可得![]() ,
,
设直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,则
,则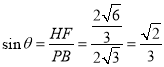 ,
,
即直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.


 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:高中数学 来源: 题型:
【题目】国际上通常用年龄中位数指标作为划分国家或地区人口年龄构成的标准:年龄中位数在20岁以下为“年轻型”人口;年龄中位数在20~30岁为“成年型”人口;年龄中位数在30岁以上为“老龄型”人口.

如图反映了我国全面放开二孩政策对我国人口年龄中位数的影响.据此,对我国人口年龄构成的类型做出如下判断:①建国以来直至2000年为“成年型”人口;②从2010年至2020年为“老龄型”人口;③放开二孩政策之后我国仍为“老龄型”人口.其中正确的是( )
A.②③B.①③C.②D.①②
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为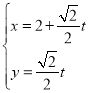 (
(![]() 为参数),曲线
为参数),曲线![]() 的参数方程为
的参数方程为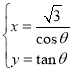 (
(![]() 为参数).
为参数).
(1)求曲线![]() ,
,![]() 的普通方程;
的普通方程;
(2)已知点![]() ,若曲线
,若曲线![]() ,
,![]() 交于
交于![]() ,
,![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,定义:以椭圆中心为圆心,长轴为直径的圆叫做椭圆的“辅助圆”.过椭圆第四象限内一点M作x轴的垂线交其“辅助圆”于点N,当点N在点M的下方时,称点N为点M的“下辅助点”.已知椭圆![]() 上的点
上的点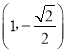 的下辅助点为(1,﹣1).
的下辅助点为(1,﹣1).
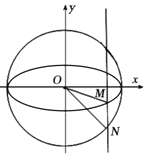
(1)求椭圆E的方程;
(2)若△OMN的面积等于![]() ,求下辅助点N的坐标;
,求下辅助点N的坐标;
(3)已知直线l:x﹣my﹣t=0与椭圆E交于不同的A,B两点,若椭圆E上存在点P,使得四边形OAPB是对边平行且相等的四边形.求直线l与坐标轴围成的三角形面积最小时的m2+t2的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】直线l:x﹣y![]() 0将圆O:
0将圆O:![]() 分成的两部分的面积之比为( )
分成的两部分的面积之比为( )
A.(4π![]() ):(8π
):(8π![]() )B.(4π﹣3
)B.(4π﹣3![]() ):(8π+3
):(8π+3![]() )
)
C.(2π﹣2![]() ):(10π+2
):(10π+2![]() )D.(2π﹣3
)D.(2π﹣3![]() ):(10π+3
):(10π+3![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 年上半年,随着新冠肺炎疫情在全球蔓延,全球超过
年上半年,随着新冠肺炎疫情在全球蔓延,全球超过![]() 个国家或地区宣布进人紧急状态,部分国家或地区直接宣布“封国”或“封城”,随着国外部分活动进入停摆,全球经济缺乏活力,一些企业开始倒闭,下表为
个国家或地区宣布进人紧急状态,部分国家或地区直接宣布“封国”或“封城”,随着国外部分活动进入停摆,全球经济缺乏活力,一些企业开始倒闭,下表为![]() 年第一季度企业成立年限与倒闭分布情况统计表:
年第一季度企业成立年限与倒闭分布情况统计表:
企业成立年份 | 2019 | 2018 | 2017 | 2016 | 2015 |
企业成立年限 | 1 | 2 | 3 | 4 | 5 |
倒闭企业数量(万家) | 5.28 | 4.72 | 3.58 | 2.70 | 2.15 |
倒闭企业所占比例 | 21.4% | 19.1% | 14.5% | 10.9% | 8.7% |
(1)由所给数据可用线性回归模型拟合![]() 与
与![]() 的关系,请用相关系数加以说明;
的关系,请用相关系数加以说明;
(2)建立![]() 关于
关于![]() 的回归方程,预测
的回归方程,预测![]() 年成立的企业中倒闭企业所占比例.
年成立的企业中倒闭企业所占比例.
参考数据:![]() ,
,![]() ,
,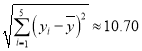 ,
,![]() ,
,
相关系数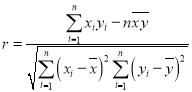 ,样本
,样本![]() 的最小二乘估计公式为
的最小二乘估计公式为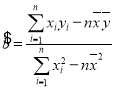 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 满足
满足![]() ,
,![]() ,其中常数
,其中常数![]() .
.
(Ⅰ)若![]() ,求
,求![]() 的取值范围;
的取值范围;
(Ⅱ)若![]() ,求证:对于任意的
,求证:对于任意的![]() ,均有
,均有![]() ;
;
(Ⅲ)当常数![]() 时,设
时,设![]() ,若存在实数
,若存在实数![]() 使得
使得![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设{an}是一个首项为2,公比为q(q![]() 1)的等比数列,且3a1,2a2,a3成等差数列.
1)的等比数列,且3a1,2a2,a3成等差数列.
(1)求{an}的通项公式;
(2)已知数列{bn}的前n项和为Sn,b1=1,且![]() 1(n≥2),求数列{an
1(n≥2),求数列{an![]() bn}的前n项和Tn.
bn}的前n项和Tn.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com