练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】“中国剩余定理”又称“孙子定理”，最早可见于中国南北朝时期的数学著作《孙子算经》卷下第二十六题，叫做“物不知数”，原文如下：今有物不知其数，三三数之剩二，五五数之剩三，七七数之剩二，问物几何？现有这样一个相关的问题：将1到2020这2020个自然数中满足被3除余2且被5除余3的数按照从小到大的顺序排成一列，构成一个数列，则该数列的项数是（ ）

    A.135B.134C.59D.58

    【答案】A

    【解析】

    根据“被3除余2且被5除余3的数”，可得这些数构成等差数列，然后根据等差数列的前项和公式，可得结果．

    被3除余2且被5除余3的数构成首项为8，公差为15的等差数列，记为， 则， 令 ，解得．

    ∴将1到2020这2020个自然数中满足被3除余2且被5除余3的数按照从小到大的顺序排成一列， 构成一个数列，则该数列的项数是135．

    故选：A．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】某生物研究所为研发一种新疫苗，在200只小白鼠身上进行科研对比实验，得到如下统计数据：

    未感染病毒

    感染病毒

    总计

    未注射疫苗

    30

    注射疫苗

    70

    总计

    100

    100

    200

    现从未注射疫苗的小白鼠中任取1只，取到“感染病毒”的小白鼠的概率为.

    （Ⅰ）能否有的把握认为注射此种疫苗有效？

    （Ⅱ）在未注射疫苗且未感染病毒与注射疫苗且感染病毒的小白鼠中，分别抽取3只进行病例分析，然后从这6只小白鼠中随机抽取2只对注射疫苗情况进行核实，求抽到的2只均是注射疫苗且感染病毒的小白鼠的概率.

    附：，，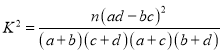

    0.10

    0.05

    0.025

    0.010

    0.005

    0.001

    2.706

    3.841

    5.024

    6.635

    7.879

    10.828

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知的内角A，B，C的对边分别为a，b，c，且，若的面积为，则的周长的最小值为（ ）

    A.4B.C.6D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x），则函数y＝f（f（x））﹣1的所有零点构成的集合为_____.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】四个同样大小的球，，，两两相切，点是球上的动点，则直线与直线所成角的正弦值的取值范围为（ ）．

    A.B.C.D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）若，求的取值范围；

    （2）若存在唯一的极小值点，求的取值范围，并证明.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】国际上通常用年龄中位数指标作为划分国家或地区人口年龄构成的标准：年龄中位数在20岁以下为“年轻型”人口；年龄中位数在20～30岁为“成年型”人口；年龄中位数在30岁以上为“老龄型”人口．

    如图反映了我国全面放开二孩政策对我国人口年龄中位数的影响．据此，对我国人口年龄构成的类型做出如下判断：①建国以来直至2000年为“成年型”人口；②从2010年至2020年为“老龄型”人口；③放开二孩政策之后我国仍为“老龄型”人口．其中正确的是（ ）

    A.②③B.①③C.②D.①②

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在等比数列中，已知设数列的前n项和为，且

    （1）求数列通项公式；

    （2）证明：数列是等差数列；

    （3）是否存在等差数列，使得对任意，都有？若存在，求出所有符合题意的等差数列；若不存在，请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

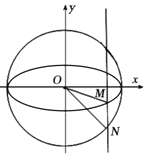
    【题目】如图，定义：以椭圆中心为圆心，长轴为直径的圆叫做椭圆的“辅助圆”．过椭圆第四象限内一点M作x轴的垂线交其“辅助圆”于点N，当点N在点M的下方时，称点N为点M的“下辅助点”．已知椭圆上的点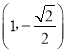的下辅助点为（1，﹣1）．

    （1）求椭圆E的方程；

    （2）若△OMN的面积等于，求下辅助点N的坐标；

    （3）已知直线l：x﹣my﹣t＝0与椭圆E交于不同的A，B两点，若椭圆E上存在点P，使得四边形OAPB是对边平行且相等的四边形．求直线l与坐标轴围成的三角形面积最小时的m2+t2的值．

    查看答案和解析>>

    同步练习册答案