
【题目】已知函数f(x)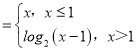 ,则函数y=f(f(x))﹣1的所有零点构成的集合为_____.
,则函数y=f(f(x))﹣1的所有零点构成的集合为_____.
【答案】{1,3,9}
【解析】
根据零点定义解方程![]() ,求出零点.
,求出零点.
函数y=f[f(x)]﹣1的零点,即求方程f[f(x)]﹣1=0的解,利用换元法进行求解即可.
解:由y=f(f(x))﹣1=0得f(f(x))=1,
设t=f(x),则等价为f(t)=1,
当x≤1时,由f(x)=x=1得x=1,
当x>1时,由f(x)=log2(x﹣1)=1得x=3,
即t=1或t=3,
当x≤1时,由f(x)=x=1,得x=1;由f(x)=x=3,得x=3(舍),故此时x=1;
当x>1时,由f(x)=log2(x﹣1)=1得x=3;由f(x)=log2(x﹣1)=3,得x=9,
综上x=1,或x=3或x=9.
所以函数y=f[f(x)]﹣1的所有零点所构成的集合为:{1,3,9}
故答案为:{1,3,9}.


 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案科目:高中数学 来源: 题型:
【题目】甲、乙两厂均生产某种零件.根据长期检测结果:甲、乙两厂生产的零件质量(单位:![]() )均服从正态分布
)均服从正态分布![]() ,在出厂检测处,直接将质量在
,在出厂检测处,直接将质量在![]() 之外的零件作为废品处理,不予出厂;其它的准予出厂,并称为正品.
之外的零件作为废品处理,不予出厂;其它的准予出厂,并称为正品.
(1)出厂前,从甲厂生产的该种零件中抽取10件进行检查,求至少有1片是废品的概率;
(2)若规定该零件的“质量误差”计算方式为:该零件的质量为![]() ,则“质量误差”
,则“质量误差”![]() .按标准,其中“优等”、“一级”、“合格”零件的“质量误差”范围分别是
.按标准,其中“优等”、“一级”、“合格”零件的“质量误差”范围分别是![]() ,
,![]() 、
、![]() (正品零件中没有“质量误差”大于
(正品零件中没有“质量误差”大于![]() 的零件),每件价格分别为75元、65元、50元.现分别从甲、乙两厂生产的正品零件中随机抽取100件,相应的“质量误差”组成的样本数据如下表(用这个样本的频率分布估计总体分布,将频率视为概率):
的零件),每件价格分别为75元、65元、50元.现分别从甲、乙两厂生产的正品零件中随机抽取100件,相应的“质量误差”组成的样本数据如下表(用这个样本的频率分布估计总体分布,将频率视为概率):
质量误差 |
|
|
|
|
|
|
|
甲厂频数 | 10 | 30 | 30 | 5 | 10 | 5 | 10 |
乙厂频数 | 25 | 30 | 25 | 5 | 10 | 5 | 0 |
(ⅰ)记甲厂该种规格的2件正品零件售出的金额为![]() (元),求
(元),求![]() 的分布列及数学期望
的分布列及数学期望![]() ;
;
(ⅱ)由上表可知,乙厂生产的该规格的正品零件只有“优等”、“一级”两种,求5件该规格零件售出的金额不少于360元的概率.
附:若随机变量![]() .则
.则![]() ;
;![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年底,湖北省武汉市等多个地区陆续出现感染新型冠状病毒肺炎的患者.为及时有效地对疫情数据进行流行病学统计分析,某地研究机构针对该地实际情况,根据该地患者是否有武汉旅行史与是否有确诊病例接触史,将新冠肺炎患者分为四类:有武汉旅行史(无接触史),无武汉旅行史(无接触史),有武汉旅行史(有接触史)和无武汉旅行史(有接触史),统计得到以下相关数据.
(1)请将列联表填写完整:
有接触史 | 无接触史 | 总计 | |
有武汉旅行史 | 27 | ||
无武汉旅行史 | 18 | ||
总计 | 27 | 54 |
(2)能否在犯错误的概率不超过0.025的前提下认为有武汉旅行史与有确诊病例接触史有关系?
附:![]()
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,过椭圆C:![]() 上一点P作x轴的垂线,垂足为
上一点P作x轴的垂线,垂足为![]() ,已知
,已知![]() ,
,![]() 分别为椭圆C的左、右焦点,A,B分别是椭圆C的右顶点、上顶点,且
分别为椭圆C的左、右焦点,A,B分别是椭圆C的右顶点、上顶点,且![]() ,
,![]() .
.
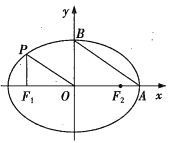
(1)求椭圆C的方程;
(2)过点![]() 的直线l交椭圆C于M,N两点,记直线PM,PN,MN的斜率分别为
的直线l交椭圆C于M,N两点,记直线PM,PN,MN的斜率分别为![]() ,问:
,问:![]() 是否为定值?请说明理由.
是否为定值?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 是
是![]() 上的奇函数,其中
上的奇函数,其中![]() ,则下 列关于函数
,则下 列关于函数![]() 的描述中,其中正确的是( )
的描述中,其中正确的是( )
①将函数![]() 的图象向右平移
的图象向右平移![]() 个单位可以得到函数
个单位可以得到函数![]() 的图象;
的图象;
②函数![]() 图象的一条对称轴方程为
图象的一条对称轴方程为![]() ;
;
③当![]() 时,函数
时,函数![]() 的最小值为
的最小值为![]() ;
;
④函数![]() 在
在![]() 上单调递增.
上单调递增.
A.①③B.③④C.②③D.②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() ,
,![]() .已知函数
.已知函数![]() ,
,![]() .
.
(Ⅰ)求![]() 的单调区间;
的单调区间;
(Ⅱ)已知函数![]() 和
和![]() 的图象在公共点(x0,y0)处有相同的切线,
的图象在公共点(x0,y0)处有相同的切线,
(i)求证:![]() 在
在![]() 处的导数等于0;
处的导数等于0;
(ii)若关于x的不等式![]() 在区间
在区间![]() 上恒成立,求b的取值范围.
上恒成立,求b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“中国剩余定理”又称“孙子定理”,最早可见于中国南北朝时期的数学著作《孙子算经》卷下第二十六题,叫做“物不知数”,原文如下:今有物不知其数,三三数之剩二,五五数之剩三,七七数之剩二,问物几何?现有这样一个相关的问题:将1到2020这2020个自然数中满足被3除余2且被5除余3的数按照从小到大的顺序排成一列,构成一个数列,则该数列的项数是( )
A.135B.134C.59D.58
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】天上有些恒星的亮度是会变化的,其中一种称为造父(型)变星,本身体积会膨胀收缩造成亮度周期性的变化.第一颗被描述的经典造父变星是在1784年.
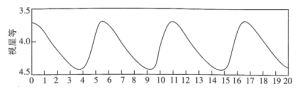
上图为一造父变星的亮度随时间的周期变化图,其中视星等的数值越小,亮度越高,则此变星亮度变化的周期、最亮时视星等,分别约是( )
A.5.5,3.7B.5.4,4.4C.6.5,3.7D.5.5,4.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,我国经济取得了长足的进步,同时性别比例问题日益突出.根据国家统计局发布的2019年统计年鉴,将国家31个省级行政区(特别行政区未记人)的人均国内生产总值与人口性别比例(每100位女性所对应的男性数目)做出了如下柱状图.从人口统计学角度来说,性别比例正常范围在102至107之间.人均国内生产总值小于6.5万元人民币(约1万美元)称为欠发达地区,大于或等于6.5万元的地区称为发达地区.
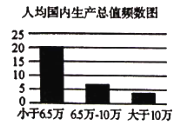
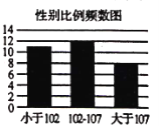
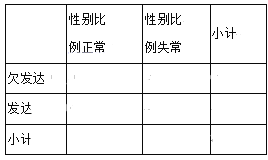
(1)已知性别比例正常的省级行政区中欠发达的行政区的个数是发达行政区的两倍,完成列联表,并判断是否有90%的把握认为各省级行政区的性别比例与经济发展程度有关;
(2)在人均国内生产总值介于6.5万与10万之间的7省级行政区中,有3个人口性别比例正常,从中任取两个,求抽到两个省级行政区的人口性别比例都正常的概率.
附:参考公式及临界值表
 ,
,![]()
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com