
【题目】已知抛物线C1的顶点在坐标原点,准线为x=﹣3,圆C2:(x﹣3)2+y2=1,过圆心C2的直线l与抛物线C1交于点A,B,l与圆C2交于点M,N,且|AM|<|AN|,则|AM|![]() |BM|的最小值为_____.
|BM|的最小值为_____.
【答案】6
【解析】
设抛物线的标准方程,将点代入抛物线方程,求得抛物线方程,由抛物线的焦点弦性质,求得![]() =
=![]() =
=![]() ,根据抛物线的定义及基本不等式,即可求得答案.
,根据抛物线的定义及基本不等式,即可求得答案.
设抛物线的方程:y2=2px(p>0),由准线方程x=﹣3,
可得![]() 3,即p=6,
3,即p=6,
抛物线的标准方程为y2=12x,焦点坐标F(3,0),
圆C2:(x﹣3)2+y2=1的圆心为(3,0),半径为1,
由直线AB过抛物线的焦点,利用极坐标,可设A(ρ1,θ),B(ρ2,π+θ),
由ρ![]() ,可得
,可得![]() ,
,
|AM|![]() |BM|=|AF|﹣1
|BM|=|AF|﹣1![]() (|BF|+1)=|AF|
(|BF|+1)=|AF|![]() |BF|
|BF|![]()
=3(![]() )(|AF|
)(|AF|![]() |BF|)
|BF|)![]()
=3(![]() )
)![]() 3(
3(![]() 2
2![]() )
)![]() 6,
6,
当且仅当|BF|=2|AF|=9时取得等号,
则|AM|![]() |BM|的最小值为6.
|BM|的最小值为6.


科目:高中数学 来源: 题型:
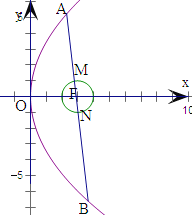
【题目】在平面直角坐标系![]() 中,以坐标原点为极点,
中,以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,曲线C1的极坐标方程为
轴正半轴为极轴建立极坐标系,曲线C1的极坐标方程为![]() ,C1上任意一点P的直角坐标为
,C1上任意一点P的直角坐标为![]() ,通过变换
,通过变换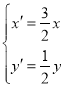 得到点P的对应点
得到点P的对应点![]() 的坐标.
的坐标.
(1)求点![]() 的轨迹C2的直角坐标方程;
的轨迹C2的直角坐标方程;
(2)直线![]() 的参数方程为
的参数方程为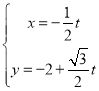 (
(![]() 为参数),
为参数),![]() 交C2于点M、N,点
交C2于点M、N,点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一块耕地上种植一种作物,每季种植成本为1000元,此作物的市场价格和这块地上的产量均具有随机性,且互不影响,其具体情况如下表:
作物产量( | 400 | 500 |
概率 |
|
|
作物市场价格(元/ | 5 | 6 |
概率 |
|
|
(1)设![]() 表示在这块地上种植1季此作物的利润,求
表示在这块地上种植1季此作物的利润,求![]() 的分布列(利润
的分布列(利润![]() 产量
产量![]() 市场价格
市场价格![]() 成本);
成本);
(2)若在这块地上连续3季种植此作物,求这3季中的利润都在区间![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高三年级有1000名学生,其中理科班学生占80%,全体理科班学生参加一次考试,考试成绩近似地服从正态分布N(72,36),若考试成绩不低于60分为及格,则此次考试成绩及格的人数约为( )
(参考数据:若Z~N(μ,σ2),则P(μ﹣σ<Z≤μ+σ)=0.6826,P(μ﹣2σ<Z<μ+2σ)=0.9544,P(μ﹣3σ<Z<μ+3σ)=0.9974)
A.778B.780C.782D.784
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex![]() .
.
(1)若f(x)的图象在x=a处切线的斜率为e﹣1,求正数a的值;
(2)对任意的a≥0,f(x)>2lnx![]() k恒成立,求整数k的最大值.
k恒成立,求整数k的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】改革开放以来,人们的支付方式发生了巨大转变.近年来,移动支付已成为主要支付方式之一.为了解某校学生上个月A,B两种移动支付方式的使用情况,从全校学生中随机抽取了100人,发现样本中A,B两种支付方式都不使用的有5人,样本中仅使用A和仅使用B的学生的支付金额分布情况如下:
支付方式 | (0,1000] | (1000,2000] | 大于2000 |
仅使用A | 18人 | 9人 | 3人 |
仅使用B | 10人 | 14人 | 1人 |
(Ⅰ)从全校学生中随机抽取1人,估计该学生上个月A,B两种支付方式都使用的概率;
(Ⅱ)从样本仅使用A和仅使用B的学生中各随机抽取1人,以X表示这2人中上个月支付金额大于1000元的人数,求X的分布列和数学期望;
(Ⅲ)已知上个月样本学生的支付方式在本月没有变化.现从样本仅使用A的学生中,随机抽查3人,发现他们本月的支付金额都大于2000元.根据抽查结果,能否认为样本仅使用A的学生中本月支付金额大于2000元的人数有变化?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)是定义在R上的偶函数,且对任意的x∈R恒有f(x+1)=f(x﹣1),已知当x∈[0,1]时,f(x)=(![]() )1﹣x,则
)1﹣x,则
①2是函数f(x)的一个周期;
②函数f(x)在(1,2)上是减函数,在(2,3)上是增函数;
③函数f(x)的最大值是1,最小值是0;
④x=1是函数f(x)的一个对称轴;
⑤当x∈(3,4)时,f(x)=(![]() )x﹣3.
)x﹣3.
其中所有正确命题的序号是_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,曲线C1:![]() ,以O为极点,x轴正半轴为极轴建立极坐标系,曲线C2是圆心极坐标为(3,π),半径为1的圆.
,以O为极点,x轴正半轴为极轴建立极坐标系,曲线C2是圆心极坐标为(3,π),半径为1的圆.
(1)求曲线C1的参数方程和C2的直角坐标方程;
(2)设M,N分别为曲线C1,C2上的动点,求|MN|的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com