��֪�Ȳ�����{an}��ͨ�ʽΪan=3n-2���ȱ�����{bn}�У�b1=a1��b4=a3+1���Ǽ���A={x|x=an��n��N*}��B={x|x=bn��n��N*}��U=A��B���Ѽ���U�е�Ԫ�ذ���С�����������У���������{cn}��
����������{bn}��ͨ�ʽ��
����������{cn}��ǰ50���S50��
���Ѽ���∁UA�е�Ԫ�ش�С�����������й�������{dn}��д������{dn}��ͨ�ʽ����˵�����ɣ�
���𰸡�
������������ȱ�����{b
n}�Ĺ���Ϊq�����õȱ����е�ͨ�ʽ�������q���Ӷ��õ�ͨ�ʽ��
����������{a
n}������{b
n}�������ٶȣ��ж�����{c
n}��ǰ50���а���{a
n}��{b
n}�����������ٸ��ݵȲ��������ʽ���ɵõ������
���ݼ���B��Ԫ��2��8��32��128∉A���²�����{d
n}��ͨ�ʽΪd
n=2
2n-1����d
n=b
2n����ֻ��֤������{b
n}�У�b
2n-1��A��b
2n∉A��n��N
*����ͨ������b
2n+1-b
2n-1�������b
2n-1��A����b
2n+1��A������Ϊb
1��A�ж�b
2n-1��A��n��N
*����ͬ�����ж�b
2n∉A���Ӷ��õ�d
n=2
2n-1��
����⣺������ȱ�����{b
n}�Ĺ���Ϊq��
��b
1=a
1=1��b
4=a
3+1=8����q
3=8����q=2��
��b
n=2
n-1��
����������{a
n}������{b
n}�������ٶȣ�����{c
n}��ǰ50������������{a
n}��ѡ50�����{a
n}��ǰ50�������ɵļ���Ϊ{1��4��7��10������148}��
��2
n-1��148�ã�n��8������{b
n}��ǰ8��ɵļ���Ϊ{1��2��4��8��16��32��64��128}������1��4��16��64�ǵȲ�����{a
n}�е��2��8��32��128���ǵȲ������е��a
46=136��128��������{c
n}��ǰ50��Ӧ��������{a
n}��ǰ46�������{b
n}�е�2��8��32��128��4�
����S
50=
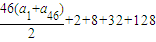
=3321��
���ݼ���B��Ԫ��2��8��32��128∉A���²�����{d
n}��ͨ�ʽΪd
n=2
2n-1��
��d
n=b
2n����ֻ��֤������{b
n}�У�b
2n-1��A��b
2n∉A��n��N
*����
֤�����£���b
2n+1-b
2n-1=2
2n-2
2n-2=4
n-4
n-1=3×4
n-1����b
2n+1=b
2n-1+3×4
n-1��
��?m��N
*��ʹb
2n-1=3m-2����ôb
2n+1=3m-2+3×4
n-1=3��m+4
n-1��-2��
���ԣ���b
2n-1��A����b
2n+1��A����Ϊb
1��A���ظ�ʹ���������ۣ�����b
2n-1��A��n��N
*����
ͬ����b
2n+2-b
2n=2
2n+1-2
2n-1=2×4
n-2×4
n-1=3×2×4
n-1����b
2n+2=b
2n+3×2×4
n-1��
��Ϊ��3×2×4
n-1������{a
n}����3����������
����˵��b
2n ��b
2n+2��n��N
*��ͬʱ����A��ͬʱ������A��
��n=1ʱ����Ȼb
2=2∉A������b
4=2∉A���ظ�ʹ���������ۣ�����b
2n∉A��
��d
n=2
2n-1��
���������⿼��Ȳ����С��ȱ����е��ۺϼ�������ͣ�����ѧ���ۺ�����֪ʶ�����������������������У������Ȳº�֤��˼·ֵ�ý��ѧϰ��Ҫϸ����ᣮ

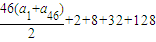 =3321��
=3321�� 

 ��������ܸ�ϰϵ�д�
��������ܸ�ϰϵ�д�
 ��֪�Ȳ�����{an}�У�a4a6=-4��a2+a8=0��n��N*��
��֪�Ȳ�����{an}�У�a4a6=-4��a2+a8=0��n��N*��