分析:(1)因为顶点在A
1底面ABC上的射影恰为点B,得到A
1B⊥AC,又AB⊥AC,利用线面垂直的判断定理可得AC⊥面AB
1B,从而可证平面A
1AC⊥平面AB
1B.
(2)建立空间直角坐标系,求出
=(0,2,2),
==(2,-2,0),利用向量的数量积公式求出棱AA
1与BC所成的角的大小;
(3)求出平面PAB的法向量为
,而平面ABA
1的法向量
=(1,0,0),利用向量的数量积公式求出二面角P-AB-A
1的平面角的余弦值.
解答:
证明:(1)∵A
1B⊥面ABC,∴A
1B⊥AC,------(1分)
又AB⊥AC,AB∩A
1B=B
∴AC⊥面AB
1B,------(3分)
∵AC?面A
1AC,
∴平面A
1AC⊥平面AB
1B;------(4分)
(2)如图,以A为原点建立空间直角坐标系,则C(2,0,0),B(02,0),A
1(0,2,2),B
1(0,4,2),
所以
=(0,2,2),
==(2,-2,0).
所以
cos<,>==-,
故AA
1与棱BC所成的角是
. …(8分)
(3)因为P为棱B
1C
1的中点,所以P的坐标为(1,3,2). …(10分)
设平面PAB的法向量为
=(x,y,z),则
令z=1故
=(-2,0,1) …(12分)
而平面ABA
1的法向量
=(1,0,0),则
|cos<,>|=
||=故二面角P-AB-A
1的平面角的余弦值是
. …(14分)
点评:本题以三棱柱为载体,考查了直线与平面垂直的判定,以及二面角及其度量和点、线、面间的距离计算,考查空间想象能力、运算能力和推理论证能力.

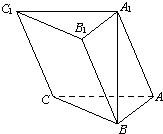 (2011•天津模拟)如图,在三棱柱ABC-A1B1C1中,AB⊥AC,顶点A1在底面ABC上的射影恰为点B,且AB=AC=A1B=2.
(2011•天津模拟)如图,在三棱柱ABC-A1B1C1中,AB⊥AC,顶点A1在底面ABC上的射影恰为点B,且AB=AC=A1B=2. 证明:(1)∵A1B⊥面ABC,∴A1B⊥AC,------(1分)
证明:(1)∵A1B⊥面ABC,∴A1B⊥AC,------(1分)

 (2011•天津模拟)已知函数f(x)=Asin(ωx+φ)(A>0,ω>0)的部分图象如图所示,则y=f(x)的图象可由函数g(x)=sinx的图象(纵坐标不变)( )
(2011•天津模拟)已知函数f(x)=Asin(ωx+φ)(A>0,ω>0)的部分图象如图所示,则y=f(x)的图象可由函数g(x)=sinx的图象(纵坐标不变)( )