
 =
=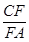 =
=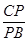 =
= (如图(1)),将△AEF沿EF折起到△
(如图(1)),将△AEF沿EF折起到△ EF的位置,使二面角
EF的位置,使二面角
 EF
EF B成直二面角,连接
B成直二面角,连接 B、
B、 P(如图(2)).
P(如图(2)).
 E⊥平面BEP;
E⊥平面BEP; E与平面
E与平面 BP所成角的大小.
BP所成角的大小. E与平面
E与平面 BP所成角的大小为
BP所成角的大小为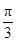 .
.
 EB为二面角
EB为二面角
 EF
EF B的平面角,根据二面角
B的平面角,根据二面角
 EF
EF B为直二面角,得到
B为直二面角,得到 E⊥BE.
E⊥BE. E⊥平面BEF,即
E⊥平面BEF,即 E⊥平面BEP.
E⊥平面BEP.
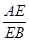 =
=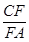 =
=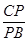 =
=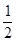 ,∴FA=AD=2.又∠A=60°,
,∴FA=AD=2.又∠A=60°, E⊥EF,BE⊥EF,∴∠
E⊥EF,BE⊥EF,∴∠ EB为二面角
EB为二面角
 EF
EF B的平面角,
B的平面角,
 EF
EF B为直二面角,∴
B为直二面角,∴ E⊥BE.
E⊥BE. E⊥平面BEF,即
E⊥平面BEF,即 E⊥平面BEP.
E⊥平面BEP. E⊥平面BEP,BE⊥EF,建立如图所示的空间直角坐标系,
E⊥平面BEP,BE⊥EF,建立如图所示的空间直角坐标系, (0,0,1),B(2,0,0).连接DP,由(1)知EF
(0,0,1),B(2,0,0).连接DP,由(1)知EF 

科目:高中数学 来源:不详 题型:单选题
| A.1 | B.2 | C.3 | D.4 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
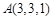 ,
,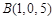 ,则下面说法中,正确的个数是 ( )
,则下面说法中,正确的个数是 ( )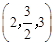 ;(2)线段AB的长度为
;(2)线段AB的长度为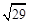 ;
;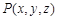 的坐标
的坐标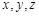 满足
满足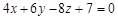 .
.| A.0个 | B.1个 | C.2个 | D.3个 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
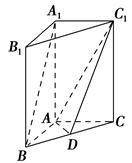
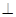 平面ABCD, AD//BC//FE,AB
平面ABCD, AD//BC//FE,AB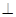 AD,M为EC的中点,AF=AB=BC=FE=
AD,M为EC的中点,AF=AB=BC=FE=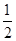 AD
AD AMD
AMD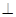 平面CDE;
平面CDE; E的余弦值.
E的余弦值.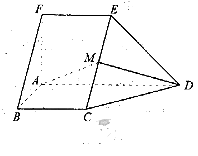
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com