
| ||
| 2 |
| OA |
| OB |
| OQ |
| 0 |
| OA |
| OB |
| OQ |
| 0 |
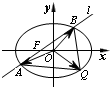
 解:(1)如图设M(x,y)、P(x0,y0),则由|DM|=m|PD|(0<m<1)得
解:(1)如图设M(x,y)、P(x0,y0),则由|DM|=m|PD|(0<m<1)得
|
| x2 |
| 4 |
| y2 |
| 4m2 |
| 1-m2 |
| ||
| 2 |
|
| 2c |
| 2m2+1 |
| 4-12m2 |
| 2m2+1 |
| ||
| 2 |
| OQ |
| OA |
| OB |
| 2c |
| 2m2+1 |
-2
| ||
| 2m2+1 |
| 2c |
| 2m2+1 |
-2
| ||
| 2m2+1 |
| x2 |
| 4 |
| y2 |
| 4m2 |
| ||
| 2 |
| ||
| 2 |


科目:高中数学 来源: 题型:
| A、①② | B、②③ | C、①④ | D、②④ |
查看答案和解析>>
科目:高中数学 来源: 题型:
| π |
| 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:
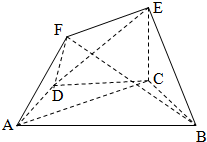 如图,在多面体ABCDEF中,底面ABCD是梯形,且满足AD=DC=CB=
如图,在多面体ABCDEF中,底面ABCD是梯形,且满足AD=DC=CB=| 1 |
| 2 |
| 1 |
| 2 |
3
| ||
| 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 甲 | 37 | 21 | 31 | 20 | 29 | 19 | 32 | 23 | 25 | 33 |
| 乙 | 10 | 30 | 47 | 27 | 46 | 14 | 26 | 10 | 44 | 46 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (文)已知中心在原点O,左焦点为F1(-1,0)的椭圆C的左顶点为A,上顶点为B,F1到直线AB的距离为
(文)已知中心在原点O,左焦点为F1(-1,0)的椭圆C的左顶点为A,上顶点为B,F1到直线AB的距离为
| ||
| 7 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com