
| A. | [$\frac{21}{4}$,7] | B. | [0,12] | C. | [3,$\frac{21}{4}$] | D. | [0,7] |
分析 作出不等式组对应的平面区域,利用作差法求出z的表达式,然后根据平移,根据数形结合即可得到结论.
解答  解:作出不等式组$\left\{\begin{array}{l}{|x|≤3,|y|≤3}\\{-4x≤y≤\frac{2x}{3}}\end{array}\right.$对应的平面区域如图阴影部分.
解:作出不等式组$\left\{\begin{array}{l}{|x|≤3,|y|≤3}\\{-4x≤y≤\frac{2x}{3}}\end{array}\right.$对应的平面区域如图阴影部分.
由y-3x的几何意义为在y轴上的纵截距,
平移直线y=3x,可得经过点(0,0)时,取得最大值0;
经过点(3,-3)时,取得最小值-12.
max{|3x-y|,x+2y}=max{3x-y,x+2y},
由y≤$\frac{2x}{3}$,可得3x-y≥x+2y,
即有z=max{3x-y,x+2y}=3x-y.
显然平移直线y=3x,可得经过点(0,0)时,z取得最小值0;
经过点(3,-3)时,z取得最大值12.
即所求取值范围是[0,12].
故选:B.
点评 本题主要考查线性规划的应用,根据z的几何意义确定对应的直线方程是截距是本题的关键,属于中档题.


科目:高中数学 来源: 题型:解答题
| 分数区间 | 4 | 5 |
| [0,30) | 0.1 | 0.2 |
| [30,60) | 0.2 | 0.2 |
| [60,90) | 0.3 | 0.4 |
| [90,120) | 0.2 | 0.1 |
| [120,150] | 0.2 | 0.1 |
| 优秀 | 不优秀 | 总计 | |
| 甲班 | 6 | 24 | 30 |
| 乙班 | 3 | 27 | 30 |
| 总计 | 9 | 51 | 60 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a≤e | B. | 0<a≤e | C. | a≥e | D. | 0<a<$\frac{1}{e}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示的多面体是由一个以四边形ABCD为地面的直四棱柱被平面A1B1C1D1所截面成,若AD=DC=2,AB=BC=2$\sqrt{3}$,∠DAB=∠BCD=90°,且AA1=CC1=$\frac{3}{2}$;
如图所示的多面体是由一个以四边形ABCD为地面的直四棱柱被平面A1B1C1D1所截面成,若AD=DC=2,AB=BC=2$\sqrt{3}$,∠DAB=∠BCD=90°,且AA1=CC1=$\frac{3}{2}$;查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 关于x轴对称的图形 | B. | 关于y轴对称的图形 | ||
| C. | 关于原点对称的图形 | D. | 关于直线y=x对称的图形 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
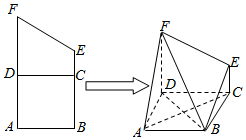 如图,梯形ABEF中,AF∥BE,AB⊥AF,且AB=BC=AD=DF=2CE=2,沿DC将梯形CDFE折起,使得平面CDFE⊥平面ABCD.
如图,梯形ABEF中,AF∥BE,AB⊥AF,且AB=BC=AD=DF=2CE=2,沿DC将梯形CDFE折起,使得平面CDFE⊥平面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 已知函数y=loga(x+b)(a,b为常数)的图象如图所示,则函数g(x)=b${\;}^{{x}^{2}-2x}$,x∈[0,3]的最大值是( )
已知函数y=loga(x+b)(a,b为常数)的图象如图所示,则函数g(x)=b${\;}^{{x}^{2}-2x}$,x∈[0,3]的最大值是( )| A. | 1 | B. | b | C. | b2 | D. | $\frac{1}{b}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x1)+f(x2)<0 | B. | f(x1)+f(x2)>0 | C. | f(x1)+f(x2)可能为0 | D. | f(x1)+f(x2)可正可负 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com