
如图:△
ABC的Ð ABC=90°,V是平面ABC外的一点,VA=VB=VC=AC,求VB与平面ABC所成的角.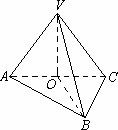
|
解:作VO^ 平面ABC于O,则OB为VB在平面ABC内的射影, ∴Ð VBO为VB与平面ABC所成的角.连 OA、OB、OC,则OA、OB、OC分别为斜线段VA、VB、VC在平面ABC内的射影.∵ VA=VB=VC∴OA=OB=OC ∴O为△ABC为外心 ∵△ ABC为直角三角形,且AC为斜边∴ O为AC的中点设 VA=a,则VA=VC=AC=a,在Rt△VOB中, 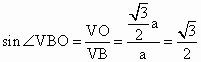
∴Ð VBO=60° ∴ VB与平面ABC所成的角为60°. |
|
1、要求VB与平面ABC所成的角,应作出它们所成的角. 2、要作出VB与平面ABC所成的角,只要找出VB在平面ABC内的射影就可以了. 3、作斜线在平面内的射影,只要在斜线上找一点作直线垂直于平面,即找此点在平面内的射影,显然找V点,V点在平面内的射影在何处?由条件可知,射影为△ABC的外心. |


科目:高中数学 来源: 题型:
 如图,△ABC的外接圆⊙O的半径为
如图,△ABC的外接圆⊙O的半径为| 5 |
| ||
| 21 |
| 2 |
| 7 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com