
| A. | Sk+1的最小值为-6 | B. | Sk+l的最大值为-6 | ||
| C. | Sk+1的最小值为6 | D. | Sk+l的最小值为6 |
分析 根据等差数列的前n项和公式,进行递推即可得到结论.
解答 解:∵Sk=ka1+k(k-1)$\frac{d}{2}$ 且Sk=kl2,
∴ka1+k(k-1)$\frac{d}{2}$=kl2,
a1+(k-1)$\frac{d}{2}$=l2…①
∵S1=la1+l(l-1)$\frac{d}{2}$ 且Sk=lk2
∴la1+l(l-1)$\frac{d}{2}$=lk2
a1+(l-1)$\frac{d}{2}$=k2…②
①-②(k-l)$\frac{d}{2}$=l2-k2
化简得 d=-2(k+l)…③
则:Sk+l=(k+l)a1+(k+l)(k+l-1)$\frac{d}{2}$,
=(k+l)[a1+(k+l-1)$\frac{d}{2}$]
=(k+l)[a1+(k-1)$\frac{d}{2}$+$\frac{d}{2}$l],
代入①、③式值:
Sk+1=-kl(k+l)
Sk+1随k,l的值增大而递减,所以Sk+1有最大值,无最小值
当k,l取最小值1,2时Sk+1最大
Sk+1(max)=-1×2(1+2)=-6,
故选:B.
点评 本题主要考查等差数列的应用,利用等差数列的通项公式以及前n项公式进行推理是解决本题的关键.综合性较强,难度较大,考查学生的运算和推理能力.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
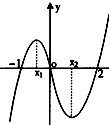
| A. | $\frac{2}{3}$ | B. | $\frac{10}{9}$ | C. | $\frac{8}{9}$ | D. | $\frac{28}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 奇函数 | B. | 偶函数 | C. | 非奇非偶函数 | D. | 既奇又偶函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 1 | C. | 0 | D. | 20152 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
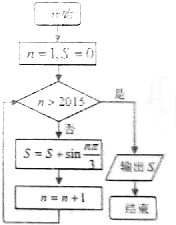 执行如图所示程序框图,则其结果输出S为( )
执行如图所示程序框图,则其结果输出S为( )| A. | 0 | B. | $\frac{\sqrt{3}}{3}$ | C. | $\sqrt{3}$ | D. | $\frac{4\sqrt{3}}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com