
已知直线l:kx-y+1+2k=0(k∈R).
(1)证明:直线l过定点;
(2)若直线l不经过第四象限,求k的取值范围;
(3)若直线l交x轴负半轴于点A,交y轴正半轴于点B,O为坐标原点,设△AOB的面积为S,求S的最小值及此时直线l的方程.
解:(1)证明:法一:直线l的方程可化为y=k(x+2)+1,
故无论k取何值,直线l总过定点(-2,1).
法二:设直线l过定点(x0,y0),
则kx0-y0+1+2k=0对任意k∈R恒成立,
即(x0+2)·k-y0+1=0恒成立,
∴x0+2=0,-y0+1=0,
解得x0=-2,y0=1,
故直线l总过定点(-2,1).
(2)直线l的方程为y=kx+2k+1,则直线l在y轴上的截距为2k+1,
要使直线l不经过第四象限,则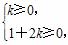
解得k的取值范围是[0,+∞).
(3)依题意,直线l在x轴上的截距为
-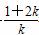 ,在y轴上的截距为1+2k,
,在y轴上的截距为1+2k,
∴A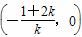 ,B(0,1+2k).
,B(0,1+2k).
又-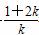 <0且1+2k>0,∴k>0.
<0且1+2k>0,∴k>0.
故S=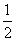 |OA||OB|=
|OA||OB|=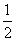 ×
×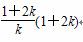
=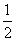
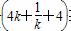 ≥
≥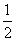 (4+4)=4,
(4+4)=4,
当且仅当4k=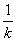 ,即k=
,即k=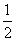 时,取等号.
时,取等号.
故S的最小值为4,
此时直线l的方程为x-2y+4=0.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案科目:高中数学 来源: 题型:
抛物线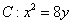 与直线
与直线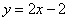 相交于
相交于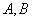 两点,点
两点,点 是抛物线
是抛物线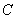 上不同
上不同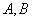 的一点,若直线
的一点,若直线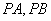 分别与直线
分别与直线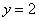 相交于点
相交于点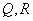 ,
,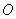 为坐标原点,则
为坐标原点,则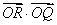 的值是
的值是
A.20 B.16 C.12 D.与点 位置有关的一个实数
位置有关的一个实数
查看答案和解析>>
科目:高中数学 来源: 题型:
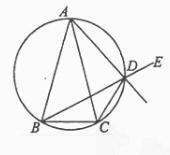 已知
已知 ABC中,AB=AC, D是
ABC中,AB=AC, D是  ABC外接圆劣弧AC弧上的点(不与点A,C重合),延长BD至E。
ABC外接圆劣弧AC弧上的点(不与点A,C重合),延长BD至E。
(1) 求证:AD的延长线平分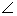 CDE;
CDE;
(2) 若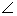 BAC=30°,
BAC=30°, ABC中BC边上的高为2+
ABC中BC边上的高为2+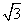 ,求
,求 ABC外接圆的面积。
ABC外接圆的面积。

查看答案和解析>>
科目:高中数学 来源: 题型:
已知两点M(2,-3),N(-3,-2),直线l过点P(1,1)且与线段MN相交,则直线l的斜率k的取值范围是( )
A.k≥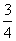 或k≤-4 B.-4≤k≤
或k≤-4 B.-4≤k≤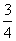
C.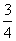 ≤k≤4 D.-
≤k≤4 D.-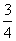 ≤k≤4
≤k≤4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com