
已知函数f(x)=x3-ax2-3x
①若f(x)在区间[1,+∞)上是增函数,求实数a的取值范围;
②若x=-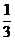 是f(x)的极值点,求f(x)在[1,a]上的最大值;
是f(x)的极值点,求f(x)在[1,a]上的最大值;
③在②的条件下,是否存在实数b,使得函数g(x)=bx的图象与f(x)的图象恰有3个交点,若存在,请求出实数b的取值范围;若不存在,试说明理由.
解:(1)f′(x)=3xax-3,…………………………1分
∵f(x)在[1,+∞)上是增函数,
∴在[1,+∞)上恒有f′(x)≥0,即3xax-3≥0在[1,+∞)上恒成立.
|
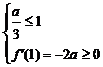 …………………………3分
…………………………3分
∴a≤0…………………………………………5分
(2)依题意,f′(-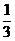 )=0,即
)=0,即 +
+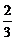 a-3=0………………………………6分
a-3=0………………………………6分
∴a=4,
∴f(x)=xxx,令f′(x)=3xx-3=0,则x1=- (舍),x2=3.………………………8分
(舍),x2=3.………………………8分
则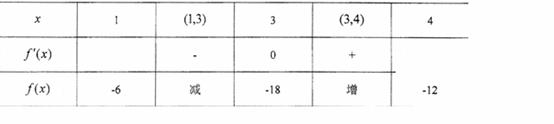
∴在[1,4]上的最大值是f(1)=-6.…………………………10分
(3)函数g(x)=bx的图象与函数f(x)的图象恰有3个交点,即方程xxx=bx恰有3个不等实根.……………………………………11分
∴xxx-bx=0, ∴x=0是其中一个根.…………………………12分
|
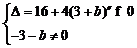 ,∴b>-7且b≠-6.………………14分
,∴b>-7且b≠-6.………………14分 

科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| x |
| a |
| b |
| x |
| 4c2 |
| k(k+c) |
查看答案和解析>>
科目:高中数学 来源:浙江省东阳中学高三10月阶段性考试数学理科试题 题型:022
已知函数f(x)的图像在[a,b]上连续不断,f1(x)=min{f(t)|a≤t≤x}(x∈[a,b]),f2(x)=max{f(t)|a≤t≤x}(x∈[a,b]),其中,min{f(x)|x∈D}表示函数f(x)在D上的最小值,max{f(x)|x∈D}表示函数f(x)在D上的最大值,若存在最小正整数k,使得f2(x)-f1(x)≤k(x-a)对任意的x∈[a,b]成立,则称函数f(x)为[a,b]上的“k阶收缩函数”.已知函数f(x)=x2,x∈[-1,4]为[-1,4]上的“k阶收缩函数”,则k的值是_________.
查看答案和解析>>
科目:高中数学 来源:上海模拟 题型:解答题
| x |
| a |
| b |
| x |
| 4c2 |
| k(k+c) |
查看答案和解析>>
科目:高中数学 来源:2009-2010学年河南省许昌市长葛三高高三第七次考试数学试卷(理科)(解析版) 题型:选择题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com