
利民商店经销某种洗衣粉,年销售量为6000包,每包进价2.80元,销售价3.40元,全年分若干次进货,每次进货x包,已知每次进货运输劳务费62.50元,全年保管费为1.5x元。
(1)把该商店经销洗衣粉一年的利润y(元)表示为每次进货量x(包)的函数,并指出函数的定义域;
(2)为了使利润最大,每次应该进货多少包?
(1)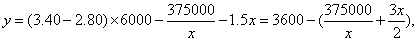
函数的定义域是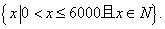 (2)500
(2)500
解析试题分析:(1)若每次进洗衣粉x包,则全年共需进洗衣粉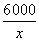 次,
次,
而全年所需运输劳务费是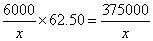 元,而全年保管费为1.5x元,
元,而全年保管费为1.5x元,
所以全年的总利润为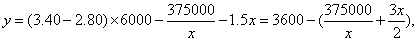
函数的定义域是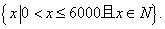
(2)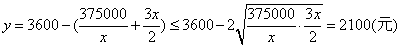
当且仅当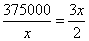 ,即当
,即当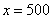 时,上式中等号成立,
时,上式中等号成立,
此时y的最大值为2100元,即为了获得最大利润2100元,每次应进洗衣粉500包。
考点:本题考查了函数的实际运用
点评:利用函数知识解数学应用问题的一般步骤是:①审题:弄清题意,分清条件和结论,理顺数量关系;②建模:将文字语言转化成数学语言,利用函数及有关数学知识,建立相应的数学模型;③求模:求解数学模型;利用数学的方法及函数的知识去解得到的数学模型,求解数学结果.④还原:将数学方法得到的结论还原为实际问题的结论,使实际问题得以解决.


科目:高中数学 来源: 题型:解答题
(本题满分13分)一艘轮船在航行中每小时的燃料费和它的速度的立方成正比,已知在速度为每小时10公里时的燃料费是每小时8元,而其他与速度无关的费用是每小时128元.
(1)求轮船航行一小时的总费用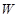 与它的航行速度
与它的航行速度 (公里/小时)的函数关系式;
(公里/小时)的函数关系式;
(2)问此轮船以多大的速度航行时,能使每公里的总费用最少?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分12分)
某市旅游部门开发一种旅游纪念品,每件产品的成本是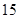 元,销售价是
元,销售价是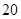 元,月平均销售
元,月平均销售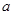 件.通过改进工艺,产品的成本不变,质量和技术含金量提高,市场分析的结果表明,如果产品的销售价提高的百分率为
件.通过改进工艺,产品的成本不变,质量和技术含金量提高,市场分析的结果表明,如果产品的销售价提高的百分率为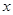
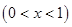 ,那么月平均销售量减少的百分率为
,那么月平均销售量减少的百分率为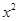 .记改进工艺后,旅游部门销售该纪念品的月平均利润是
.记改进工艺后,旅游部门销售该纪念品的月平均利润是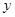 (元).
(元).
(1)写出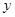 与
与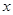 的函数关系式;
的函数关系式;
(2)改进工艺后,确定该纪念品的售价,使旅游部门销售该纪念品的月平均利润最大.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某服装厂某年1月份、2月份、3月份分别生产某名牌衣服1万件、 万件、
万件、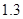 万件,为了估测当年每个月的产量,以这三个月的产品数量为依据,用一个函数模型模拟该产品的月产量
万件,为了估测当年每个月的产量,以这三个月的产品数量为依据,用一个函数模型模拟该产品的月产量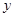 与月份
与月份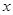 的关系,模拟函数可选用函数
的关系,模拟函数可选用函数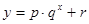 (其中
(其中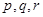 为常数)或二次函数。又已知当年4月份该产品的产量为
为常数)或二次函数。又已知当年4月份该产品的产量为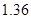 万件,请问用以上哪个函数作为模拟函数较好,并说明理由。
万件,请问用以上哪个函数作为模拟函数较好,并说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分13分))
京广高铁于2012年12月26日全线开通运营,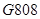 次列车在平直的铁轨上匀速行驶,由于遇到紧急情况,紧急刹车时列车行驶的路程
次列车在平直的铁轨上匀速行驶,由于遇到紧急情况,紧急刹车时列车行驶的路程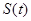 (单位:
(单位: )和时间
)和时间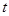 (单位:
(单位: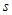 )的关系为:
)的关系为: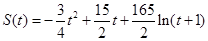 .
.
(1)求从开始紧急刹车至列车完全停止所经过的时间;
(2)求列车正常行驶的速度;
(3)求紧急刹车后列车加速度绝对值的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分12分)某民营企业生产A、B两种产品,根据市场调查和预测,A产品的利润y与投资额x成正比,其关系如图1所示;B产品的利润y与投资额x的算术平方根成正比,其关系如图2所示(利润与投资额的单位均为万元). (1)分别将A、B两种产品的利润表示为投资额的函数关系式;(2)该企业已筹集到10万元资金,并全部投入A、B两种产品的生产,问:怎样分配这10万元投资,才能使企业获得最大利润,其最大利润为多少万元?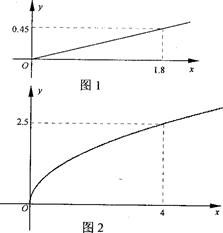
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
已知函数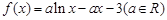 .
.
(I)当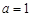 时,求函数
时,求函数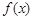 的单调区间;
的单调区间;
(II)若函数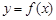 的图象在点
的图象在点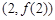 处的切线的倾斜角为45o,问:m在什么范围取值时,对于任意的
处的切线的倾斜角为45o,问:m在什么范围取值时,对于任意的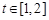 ,函数
,函数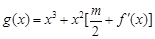 在区间
在区间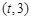 上总存在极值?
上总存在极值?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
燕子每年秋天都要从北方飞到南方过冬。研究燕子的科学家发现,两岁燕子的飞行速度可以表示为函数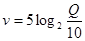 ,单位是
,单位是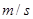 ,其中
,其中 表示燕子的耗氧量。
表示燕子的耗氧量。
(1)计算:两岁燕子静止时的耗氧量是多少个单位?(5分)
(2)当一只两岁燕子的耗氧量是80个单位时,它的飞行速度是多少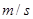 ?(5分)
?(5分)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com