
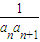 }的前n项和为Sn.
}的前n项和为Sn.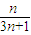 ,假设存在正整数m、n,且1<m<n,使得S1、Sm、Sn成等比数列,可求得n=
,假设存在正整数m、n,且1<m<n,使得S1、Sm、Sn成等比数列,可求得n=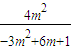 ,从而得1<m<1+
,从而得1<m<1+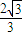 <3,由m∈N*,可求得m=2,继而可求得n.
<3,由m∈N*,可求得m=2,继而可求得n.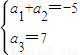 ,即
,即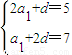 …2
…2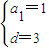 …3
…3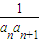 =
=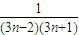 =
= (
( -
-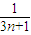 )…5
)…5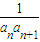 }的前n项和
}的前n项和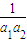 +
+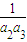 +…+
+…+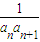
 (1-
(1- )+
)+ (
( -
- )+
)+ (
( -
- )+…+
)+…+ (
(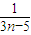 -
-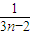 )+
)+ (
(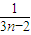 -
-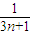 )
) (1-
(1-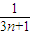 )=
)=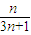 …7
…7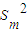 =S1•Sn…8
=S1•Sn…8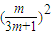 =
= ×
×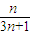 …9
…9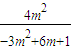 ,
,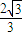 <3,
<3,

 阅读快车系列答案
阅读快车系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com