
(本小题14分)
已知函数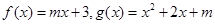
(1)求证:函数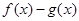 必有零点
必有零点
(2)设函数
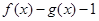 ,若
,若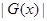 在
在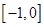 上是减函数,求实数
上是减函数,求实数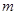 的取值范围
的取值范围
科目:高中数学 来源: 题型:
 (本小题14分)右图是一个直三棱柱(以
(本小题14分)右图是一个直三棱柱(以![]() 为底面)
为底面)
被一平面所截得到的几何体,截面为ABC.
已知![]() .
.
(1)设点O是AB的中点,证明:OC∥平面A1B1C1;
(2)证明BC⊥AC,求二面角B―AC―A1的大小;
(3)求此几何体的体积.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年广东省肇庆市高三复习必修五综合练习 题型:解答题
(本小题14分)如图所示,L是海面上一条南北方向的海防警戒线,在L上点A处有一个水声监测点,另两个监测点B,C分别在A的正东方20 km处和54 km处.某时刻,监测点B收到发自静止目标P的一个声波,8s后监测点A,20 s后监测点C相继收到这一信号.在当时气象条件下,声波在水中的传播速度是1. 5 km/s.
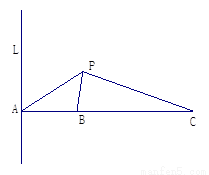
(1)设A到P的距离为 km,用
km,用 分别表示B、C到P 的距离,并求
分别表示B、C到P 的距离,并求 值;
值;
(2)求静止目标P到海防警戒线L的距离(结果精确到0.01 km)
查看答案和解析>>
科目:高中数学 来源:2011-2012学年广东省肇庆市高三复习必修五综合练习 题型:解答题
(本小题14分)在等差数列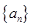 中,
中,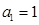 ,前
,前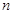 项和
项和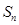 满足条件
满足条件 ,
,
(1)求数列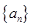 的通项公式和
的通项公式和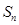 ;
;
(2)记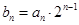 ,求数列
,求数列 的前
的前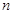 项和
项和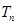
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com