
 满足
满足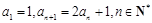 .
. 为等比数列,并求出数列
为等比数列,并求出数列 的通项公式;
的通项公式; 满足
满足 .证明:数列
.证明:数列 是等差数列.
是等差数列. .
.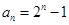 ;(2)详见解析;(3)详见解析.
;(2)详见解析;(3)详见解析. 为等比数列,就是证明
为等比数列,就是证明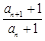 为一个常数. 因为
为一个常数. 因为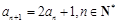 ,所以
,所以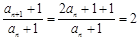 ,所以,
,所以,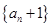 是以2为首项,2为公比的等比数列. 则
是以2为首项,2为公比的等比数列. 则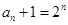 ,即
,即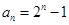 ,
,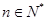 ;(2)证明数列
;(2)证明数列 是等差数列,就是要证明
是等差数列,就是要证明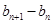 为一个常数.首先化简等式
为一个常数.首先化简等式 ,即
,即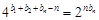 ,所以
,所以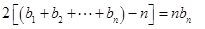 ,这实质是
,这实质是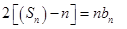 ,因此作差消去
,因此作差消去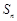 得:
得: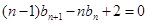 ,再作差消去常数得:
,再作差消去常数得: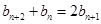 ,
,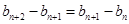 ,即
,即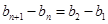 ;(3)证明数列不等式,一般有两个思路,一是求和,二是放缩.本题由于通项
;(3)证明数列不等式,一般有两个思路,一是求和,二是放缩.本题由于通项 不适宜求和,所以尝试放缩,即利用变量分离进行放缩,由
不适宜求和,所以尝试放缩,即利用变量分离进行放缩,由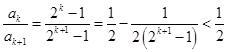 ,得
,得 .
.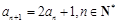 ,所以
,所以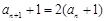 ,且
,且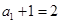 ,
,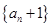 是以2为首项,2为公比的等比数列. 2分
是以2为首项,2为公比的等比数列. 2分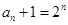 ,即
,即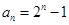 ,
,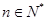 . 3分
. 3分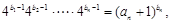 所以.
所以.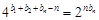 4分
4分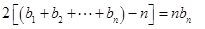 ①
①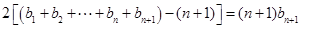 ② 6分
② 6分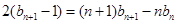
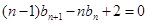 ③
③ 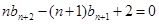 ④ 8分
④ 8分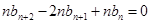 ,
,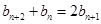
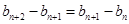 ,
,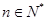 10分
10分 为等差数列.
为等差数列.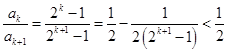 ,
,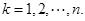 11分
11分 . 12分
. 12分

科目:高中数学 来源:不详 题型:解答题
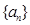 中抽出一些项,依原来的顺序组成的新数列叫数列
中抽出一些项,依原来的顺序组成的新数列叫数列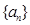 的一个子列.
的一个子列.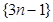 的一个是等比数列的子列;
的一个是等比数列的子列;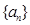 是无穷等比数列,首项
是无穷等比数列,首项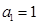 ,公比
,公比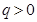 且
且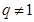 ,则数列
,则数列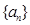 是否存在一个子列
是否存在一个子列查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 间的整数
间的整数 为分子,以
为分子,以 为分母组成分数集合
为分母组成分数集合 ,其所有元素和为
,其所有元素和为 ;以
;以 间的整数
间的整数 为分子,以
为分子,以 为分母组成不属于集合
为分母组成不属于集合 的分数集合
的分数集合 ,其所有元素和为
,其所有元素和为 ;……,依次类推以
;……,依次类推以 间的整数
间的整数 为分子,以
为分子,以 为分母组成不属于
为分母组成不属于 的分数集合
的分数集合 ,其所有元素和为
,其所有元素和为 ;则
;则 =________.
=________.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com