
已知椭圆![]() +
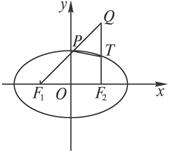
+![]() =1(a>b>0)的左、右焦点分别是F1(-c,0)、F2(c,0),点Q为椭圆外的动点,满足
=1(a>b>0)的左、右焦点分别是F1(-c,0)、F2(c,0),点Q为椭圆外的动点,满足
|![]() |=2a,点P是线段F1Q与椭圆的交点,点T在线段F2Q上,并且满足
|=2a,点P是线段F1Q与椭圆的交点,点T在线段F2Q上,并且满足![]() =0,|
=0,|![]() |≠0.
|≠0.
(1)设x为点P的横坐标,证明|![]() |=a+
|=a+![]() x.
x.
(2)求点T的轨迹C的方程.
(3)试问:在点T的轨迹C上,是否存在点M,使△F1MF2的面积S=b2?若存在,求∠F1MF2的正切值;若不存在,请说明理由.
(1)证明:设P(x,y),左准线:x=-![]() ,由椭圆第二定义
,由椭圆第二定义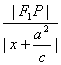 =
=![]() ,
,
∴|F1P|=![]() |x+
|x+![]() |=|a+
|=|a+![]() x|.
x|.
∵x≥-a,a>-c,
∴a+![]() x≥a-c>0.
x≥a-c>0.
∴|F1P|=a+![]() x.
x.
(2)解:设T(x,y),当|PT|=0时,点(a,0),点(-a,0)在轨迹上.当|PT|≠0时,
∵|F2T|≠0且![]() =0,
=0,
∴PT⊥TF2.
又|PQ|=|PF2|,
∴点T为QF2的中点.
在△F1F2Q中,|![]() |=
|=![]() |
|![]() |=a,
|=a,
∴x2+y2=a2,|PT|=0时也满足,
∴所求动点T的轨迹方程为x2+y2=a2.
(3)解:设C上存在点M(x0,y0)使S=b2![]()
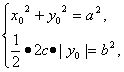
由此得|y0|≤a,及|y0|≤![]() ,
,
∴当a≥![]() 时,存在点M使S=b2;
时,存在点M使S=b2;
当a<![]() 时,不存在点M;
时,不存在点M;
当a≥![]() 时,
时,![]() =(-c-x0,-y0),
=(-c-x0,-y0),![]() =(c-x0,-y0).
=(c-x0,-y0).
由![]() ·
·![]() =x02+y02-c2=a2-c2=b2,
=x02+y02-c2=a2-c2=b2,
∴![]() ·
·![]() =|
=|![]() ||
||![]() |cos∠F1MF2,而S=
|cos∠F1MF2,而S=![]() |
|![]() ||
||![]() |sin∠F1MF2=b2,得
|sin∠F1MF2=b2,得
tan∠F1MF2=2.


科目:高中数学 来源: 题型:
A.sin30° B.cos30° C.tan30° D.sin45°
查看答案和解析>>
科目:高中数学 来源: 题型:
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com