
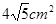 的面积,问应如何设计十字型宽
的面积,问应如何设计十字型宽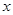 及长
及长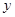 ,才能使其外接圆的周长最短,这样可使绕在铁芯上的铜线最节省.
,才能使其外接圆的周长最短,这样可使绕在铁芯上的铜线最节省.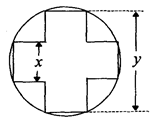
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案科目:高中数学 来源:不详 题型:解答题
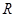 上的函数
上的函数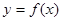 ,
,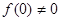 ,当
,当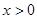 时,
时,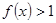 .且对任意的
.且对任意的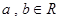 有
有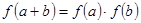 。
。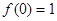 ;
;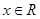 ,恒有
,恒有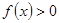 ;
;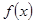 是
是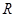 上的增函数;
上的增函数;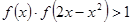 ,求
,求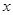 的取值范围。
的取值范围。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
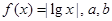 为实数,且
为实数,且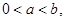
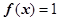 的解;
的解;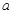 ,
,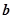 满足
满足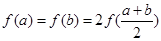 ,试写出
,试写出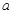 与
与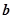 的等量关系(至少写出两个);
的等量关系(至少写出两个);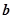 满足
满足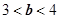 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
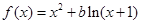 .
.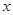 ,都有
,都有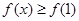 成立,求实数
成立,求实数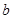 的值;
的值;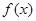 在定义域上是单调函数,求
在定义域上是单调函数,求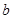 的范围;
的范围;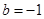 ,证明对任意正整数
,证明对任意正整数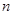 ,不等式
,不等式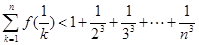 都成立.
都成立.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
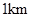 的正方形
的正方形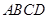 地段进行市场开发,拟在该地段的一角建设一个景观,需要建一条道路
地段进行市场开发,拟在该地段的一角建设一个景观,需要建一条道路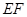 (点
(点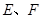 分别在
分别在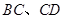 上),根据规划要求
上),根据规划要求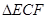 的周长为
的周长为 .
.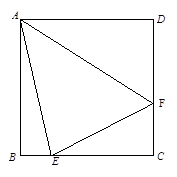
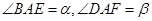 ,求证:
,求证: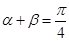 ;
;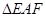 的面积最小,试确定点
的面积最小,试确定点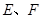 的位置.
的位置.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com