
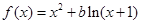 .
.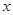 ,都有
,都有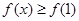 成立,求实数
成立,求实数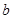 的值;
的值;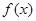 在定义域上是单调函数,求
在定义域上是单调函数,求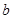 的范围;
的范围;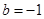 ,证明对任意正整数
,证明对任意正整数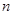 ,不等式
,不等式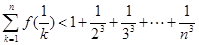 都成立.
都成立.科目:高中数学 来源:不详 题型:解答题
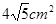 的面积,问应如何设计十字型宽
的面积,问应如何设计十字型宽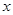 及长
及长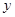 ,才能使其外接圆的周长最短,这样可使绕在铁芯上的铜线最节省.
,才能使其外接圆的周长最短,这样可使绕在铁芯上的铜线最节省.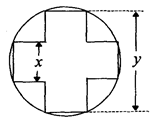
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
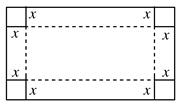
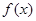 ,并指出函数
,并指出函数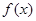 的定义域;
的定义域;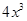 立方米的同时,又使得底面积最大,求x的值.
立方米的同时,又使得底面积最大,求x的值.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
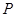 (元)之间的关系为
(元)之间的关系为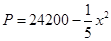 ,且生产
,且生产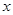 吨的成本为
吨的成本为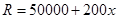 (元).问该厂每月生产多少吨产品才能使利润达到最大?最大利润是多少?(利润=收入-成本)
(元).问该厂每月生产多少吨产品才能使利润达到最大?最大利润是多少?(利润=收入-成本)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com