
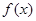 在
在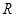 上是减函数,则满足
上是减函数,则满足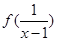 >
>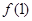 的实数
的实数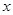 的取值范围是( ).
的取值范围是( ).| A.(-∞,1) | B.(2,+∞) |
| C.(-∞,1)∪(2,+∞) | D.(1,2) |
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:高中数学 来源:不详 题型:解答题
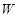 与它的航行速度
与它的航行速度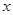 (公里/小时)的函数关系式;
(公里/小时)的函数关系式;查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
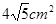 的面积,问应如何设计十字型宽
的面积,问应如何设计十字型宽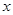 及长
及长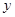 ,才能使其外接圆的周长最短,这样可使绕在铁芯上的铜线最节省.
,才能使其外接圆的周长最短,这样可使绕在铁芯上的铜线最节省.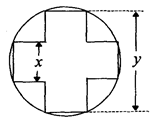
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
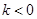 ,函数
,函数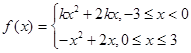
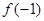 ,
,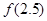 的值;
的值;  在
在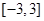 上的单调性;
上的单调性; 在
在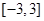 上的最小值与最大值,并求出相应的自变量的取值.
上的最小值与最大值,并求出相应的自变量的取值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com