

���� ��1�����ȡ��100��ѧ���д�һѧ����x�ˣ����õȿ����¼����ʼ��㹫ʽ�г����̣��ɴ��������ȡ��100��ѧ���д�һѧ����30�ˣ�
��2������Ƶ�ʷֲ�ֱ��ͼ�������У��ѧ��ÿ��ʹ�ù���������ƽ��ʱ�䣮
��3����100�������У������ȡ5�ˣ�ʹ�ù�������ʱ���ڣ�6��8]Сʱ�ڵ���4�ˣ���ΪA��B��C��D���ڣ�8��10]Сʱ����1�ˣ���ΪX������5������ѡ2�ˣ������оٷ��������2��ʹ�ù�������ʱ�䶼������8Сʱ�ĸ��ʣ�
��� �⣺��1�����ȡ��100��ѧ���д�һѧ����x�ˣ�
��$\frac{x}{2400}=\frac{100}{8000}$�����x=30��
���ȡ��100��ѧ���д�һѧ����30�ˣ�
��2������Ƶ�ʷֲ�ֱ��ͼ֪��У��ѧ��ÿ��ʹ�ù���������ƽ��ʱ��Ϊ��
$\overline{x}$=1��0.050��2+3��0.200��2+5��0.125��2+7��0.100��2+9��0.025��2=4.4��
���У��ѧ��ÿ��ʹ�ù���������ƽ��ʱ��Ϊ4.4Сʱ��
��3����100�������У������ȡ5�ˣ�ʹ�ù�������ʱ���ڣ�6��8]Сʱ�ڵ���4�ˣ���ΪA��B��C��D��
�ڣ�8��10]Сʱ����1�ˣ���ΪX��
����5������ѡ2�ˣ���ͬ��ѡ����10�֣��ֱ�Ϊ��
��A��B������A��C������A��D������A��X������B��C������B��D������B��X������C��D������C��X������D��X����
��2��ʹ�ù�������ʱ�䶼������8Сʱ��ѡ����6�֣��ֱ�Ϊ��
��A��B������A��C������A��D������B��C������B��D������C��D����
����2��ʹ�ù�������ʱ�䶼������8Сʱ�ĸ���p=$\frac{6}{10}=\frac{3}{5}$��
���� ���⿼����ʡ��оٷ����ŵ���͵Ȼ���֪ʶ���������ݴ�������������������������鼯��˼�롢������ת��˼�룬�ǻ����⣮


 ��ĩ1�����ʽ���������ϵ�д�
��ĩ1�����ʽ���������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
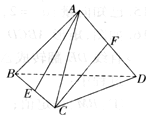 ��ͼ����������ABCD�У�E��F�ֱ�����BC��AD���е㣬��ֱ��AE��CF���ɵĽǵ�����ֵΪ��������
��ͼ����������ABCD�У�E��F�ֱ�����BC��AD���е㣬��ֱ��AE��CF���ɵĽǵ�����ֵΪ��������| A�� | $\frac{1}{3}$ | B�� | $\frac{2}{3}$ | C�� | $\frac{1}{4}$ | D�� | $\frac{3}{4}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
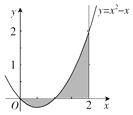
| A�� | $\frac{1}{2}$ | B�� | $\frac{2}{3}$ | C�� | 1 | D�� | $\frac{7}{6}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 8�� | B�� | 6�� | C�� | 4�� | D�� | 2�� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com