
【题目】已知函数 f ( x )=sin(2x+ ![]() )+cos(2x+
)+cos(2x+ ![]() )+2sin x cos x.
)+2sin x cos x.
(Ⅰ)求函数 f ( x) 图象的对称轴方程;
(Ⅱ)将函数 y=f ( x) 的图象向右平移 ![]() 个单位,再将所得图象上各点的横坐标伸长为原来的 4 倍,纵坐标不变,得到函数 y=g ( x) 的图象,求 y=g ( x) 在[
个单位,再将所得图象上各点的横坐标伸长为原来的 4 倍,纵坐标不变,得到函数 y=g ( x) 的图象,求 y=g ( x) 在[ ![]() ,2π]上的值域.
,2π]上的值域.
【答案】解:(Ⅰ)∵f ( x )=sin(2x+ ![]() )+cos(2x+
)+cos(2x+ ![]() )+2sinxcosx =
)+2sinxcosx = ![]() sin2x+
sin2x+ ![]() cos2x+
cos2x+ ![]() cos2x﹣
cos2x﹣ ![]() sin2x+sin2x
sin2x+sin2x
= ![]() cos2x+sin2x
cos2x+sin2x
=2sin(2x+ ![]() ),
),
∴令2x+ ![]() =kπ+
=kπ+ ![]() ,k∈Z,解得函数 f ( x) 图象的对称轴方程:x=
,k∈Z,解得函数 f ( x) 图象的对称轴方程:x= ![]() +
+ ![]() ,k∈Z,
,k∈Z,
(Ⅱ)将函数 y=f ( x) 的图象向右平移 ![]() 个单位,可得函数解析式为:y=2sin[2(x﹣
个单位,可得函数解析式为:y=2sin[2(x﹣ ![]() )+
)+ ![]() ]=2sin(2x+
]=2sin(2x+ ![]() ),
),
再将所得图象上各点的横坐标伸长为原来的 4 倍,纵坐标不变,得到函数 解析式为:y=g ( x)=2sin( ![]() +
+ ![]() ),
),
∵x∈[ ![]() ,2π],
,2π],
∴ ![]() +
+ ![]() ∈[
∈[ ![]() ,
, ![]() ],可得:sin(
],可得:sin( ![]() +
+ ![]() )∈[﹣
)∈[﹣ ![]() ,1],
,1],
∴g ( x)=2sin( ![]() +
+ ![]() )∈[﹣1,2]
)∈[﹣1,2]
【解析】(Ⅰ)利用三角函数恒等变换的应用化简函数解析式可得f ( x )=2sin(2x+ ![]() ),令2x+
),令2x+ ![]() =kπ+
=kπ+ ![]() ,k∈Z,解得函数 f ( x) 图象的对称轴方程.(Ⅱ)利用函数y=Asin(ωx+φ)的图象变换规律可求g ( x)=2sin(
,k∈Z,解得函数 f ( x) 图象的对称轴方程.(Ⅱ)利用函数y=Asin(ωx+φ)的图象变换规律可求g ( x)=2sin( ![]() +
+ ![]() ),由x∈[
),由x∈[ ![]() ,2π],利用正弦函数的性质可求值域.
,2π],利用正弦函数的性质可求值域.
【考点精析】关于本题考查的函数y=Asin(ωx+φ)的图象变换,需要了解图象上所有点向左(右)平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的横坐标伸长(缩短)到原来的
的图象上所有点的横坐标伸长(缩短)到原来的![]() 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的纵坐标伸长(缩短)到原来的
的图象上所有点的纵坐标伸长(缩短)到原来的![]() 倍(横坐标不变),得到函数
倍(横坐标不变),得到函数![]() 的图象才能得出正确答案.
的图象才能得出正确答案.


 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案科目:高中数学 来源: 题型:
【题目】在队内羽毛球选拔赛中,选手M与B1 , B2 , B3三位选手分别进行一场对抗赛,按以往多次比赛的统计,M获胜的概率分别为 ![]() ,且各场比赛互不影响.
,且各场比赛互不影响.
(1)若M至少获胜两场的概率大于 ![]() ,则M入选下一轮,否则不予入选,问M是否会入选下一轮?
,则M入选下一轮,否则不予入选,问M是否会入选下一轮?
(2)求M获胜场数X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知O为坐标原点,F是双曲线 ![]() 的左焦点,A,B分别为Γ的左、右顶点,P为Γ上一点,且PF⊥x轴,过点A的直线l与线段PF交于点M,与y轴交于点E,直线 BM与y轴交于点N,若|OE|=2|ON|,则 Γ的离心率为( )
的左焦点,A,B分别为Γ的左、右顶点,P为Γ上一点,且PF⊥x轴,过点A的直线l与线段PF交于点M,与y轴交于点E,直线 BM与y轴交于点N,若|OE|=2|ON|,则 Γ的离心率为( )
A.3
B.2
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)=xex(e为自然对数的底数),g(x)=(x+1)2 .
(I)记 ![]() ,讨论函F(x)单调性;
,讨论函F(x)单调性;
(II)令G(x)=af(x)+g(x)(a∈R),若函数G(x)有两个零点.
(i)求参数a的取值范围;
(ii)设x1 , x2是G(x)的两个零点,证明x1+x2+2<0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆Γ: ![]() +y2=1(a>1)的左焦点为F1 , 右顶点为A1 , 上顶点为B1 , 过F1 , A1 , B1三点的圆P的圆心坐标为(
+y2=1(a>1)的左焦点为F1 , 右顶点为A1 , 上顶点为B1 , 过F1 , A1 , B1三点的圆P的圆心坐标为( ![]() ,
, ![]() ).
).
(Ⅰ)求椭圆的方程;
(Ⅱ)若直线l:y=kx+m(k,m为常数,k≠0)与椭圆Γ交于不同的两点M和N.
(i)当直线l过E(1,0),且 ![]() +2
+2 ![]() =
= ![]() 时,求直线l的方程;
时,求直线l的方程;
(ii)当坐标原点O到直线l的距离为 ![]() 时,求△MON面积的最大值.
时,求△MON面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC﹣A1B1C1中,CA=CB=AA1 , ∠BAA1=∠BAC=60°,点O是线段AB的中点. (Ⅰ)证明:BC1∥平面OA1C;
(Ⅱ)若AB=2,A1C= ![]() ,求二面角A﹣BC﹣A1的余弦值.
,求二面角A﹣BC﹣A1的余弦值.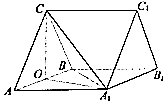
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,PA⊥圆O所在的平面,AB是圆O的直径,C是圆O上的一点,E、F分别是点A在PB、PC上的射影,给出下列结论: ①AF⊥PB;②EF⊥PB;③AF⊥BC;④AE⊥平面PBC;⑤平面PBC⊥平面PAC.其中正确命题的序号是 . 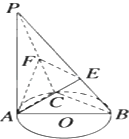
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com