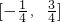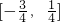练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    在△ABC中，若B=30°，则cosAsinC的取值范围是


    1. A.
      [-1，1]
    2. B.
      数学公式
    3. C.
      数学公式
    4. D.
      数学公式
    C
    分析：先利用和差化积公式对cosAcosC展开，化简整理求得cosAcosC=-sin（A-C），进而利用正弦函数的性质求得sin（A-C）的范围，进而求得cosAcosC的范围．
    解答：cosAcosC=[sin（A+C）-sin（A-C）]=[sin（π-B）-sin（A-C）]=-sin（A-C）
    因为-1≤sin（A-C）≤1
    所以-≤-sin（A-C）≤
    即cosAsinC的取值范围为
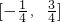
    故选C．
    点评：本题主要考查了和差化积公式的应用，正弦函数的值域问题等．考查了学生对三角函数基础知识的掌握和灵活运用．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    在△ABC中，若b=5，C=
    π
    4
    ，a=2
    		2
    ，则sinA=（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在△ABC中，若∠B=135°，AC=
    		2
    ，则三角形外接圆的半径是（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在△ABC中，若B=2A，a：b=1：
    		3
    ，则A=
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在△ABC中，若B、C的对边边长分别为b、c，B=45°，c=2
    		2
    ，b=
    4
    		3
    3
    ，则C等于（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在△ABC中，若b=12，A=30°，B=120°，则a=（　　）

    查看答案和解析>>

    同步练习册答案