
已知 .
.
(1)当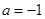 ,
, ,
, 时,求
时,求 的解集;
的解集;
(2)当 ,且当
,且当 时,
时, 恒成立,求实数
恒成立,求实数 的最小值.
的最小值.
(1) ,或
,或 (2)
(2)
解析试题分析:(1)由已知得不等式 是一个一元二次不等式,用因式分解方法可写出此不等式的解集;(2)因为
是一个一元二次不等式,用因式分解方法可写出此不等式的解集;(2)因为 ,由二次函数的零点式可将函数
,由二次函数的零点式可将函数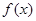 的解析式写成:
的解析式写成: ,从而当
,从而当 时,
时, 恒成立等价于
恒成立等价于 在
在 恒成立,通过分离参数a,将恒成立问题转化为函数的最值问题加以解决;或结合二次函数的图象,通过分类讨论求得字母a的取值范围.
恒成立,通过分离参数a,将恒成立问题转化为函数的最值问题加以解决;或结合二次函数的图象,通过分类讨论求得字母a的取值范围.
试题解析:(1)当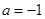 ,
, ,
, 时,
时, ,即
,即 ,
,  ,
, ,或
,或 .
.
(2)因为 ,所以
,所以 ,
, 在
在 恒成立,
恒成立,
即 在
在 恒成立,
恒成立,
而
当且仅当 ,即
,即 时取到等号. ,
时取到等号. ,
所以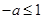 ,即
,即 .所以
.所以 的最小值是
的最小值是
(2)或解: 在
在 恒成立,
恒成立,
即 在
在 恒成立.
恒成立.
令 .
.
①当 时,
时, 在
在 上恒成立,符合;
上恒成立,符合;
②当 时,易知在
时,易知在 上恒成立,符合;
上恒成立,符合;
③当 时,则
时,则 ,所以
,所以 .
.
综上所述,
所以 的最小值是
的最小值是 .
.
考点:1.一元二次不等式;2.不等式的恒成立.


 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:高中数学 来源: 题型:解答题
如图(1)所示,将边长为1的正六边形铁皮的六个角各切去一个全等的四边形,再沿虚线折起,做成一个无盖的正六棱柱容器,如图(2)所示,求这个正六棱柱容器容积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com