
某工厂某种产品的年固定成本为250万元,每生产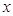 千件,需另投入成本为
千件,需另投入成本为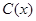 (万元),当年产量不足80千件时,
(万元),当年产量不足80千件时,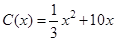 (万元).当年产量不小于80千件时,
(万元).当年产量不小于80千件时,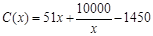 (万元).每件商品售价为500元.通过市场分析,该厂生产的商品能全部售完.
(万元).每件商品售价为500元.通过市场分析,该厂生产的商品能全部售完.
(1)写出年利润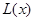 (万元)关于年产量
(万元)关于年产量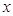 (千件)的函数解析式;
(千件)的函数解析式;
(2)年产量为多少千件时,该厂在这一商品的生产中所获利润最大?
(1)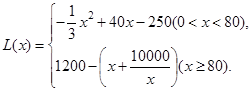 ;(2)当
;(2)当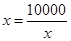 时,即
时,即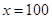 时
时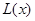 取得最大值1000万元.
取得最大值1000万元.
解析试题分析:
对于有关利润的题目,要注意总销售额、成本,利润=总销售额-总成本,在题目中,如果含有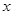 的范围有几段,则要分论,函数写成分段函数形式;则由题知每件商品售价为0.05万元,则
的范围有几段,则要分论,函数写成分段函数形式;则由题知每件商品售价为0.05万元,则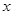 千件商品销售额为
千件商品销售额为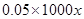 万元,在
万元,在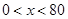 时,年利润
时,年利润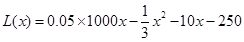 ;在
;在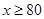 ,年利润
,年利润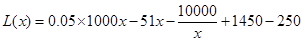 ,整理好结果用分段函数表示;(2)求利润最大,即是求函数的最大值,由于是分段函数,则分别求出每段函数的最大值,最终比较两段最大中的较大者,即是函数最大;由(1)可求
,整理好结果用分段函数表示;(2)求利润最大,即是求函数的最大值,由于是分段函数,则分别求出每段函数的最大值,最终比较两段最大中的较大者,即是函数最大;由(1)可求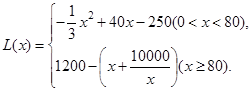 则在
则在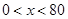 时用二次函数的方法求最大,注意
时用二次函数的方法求最大,注意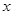 的范围,在
的范围,在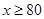 中,利用均值不等式求出,注意等号成立的条件.
中,利用均值不等式求出,注意等号成立的条件.
试题解析:(1)由题知每件商品售价为0.05万元,则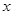 千件商品销售额为
千件商品销售额为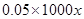 万元,
万元,
当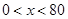 时,年利润
时,年利润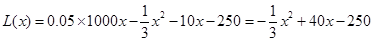 ;
;
当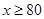 ,年利润
,年利润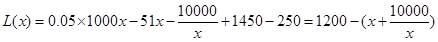
则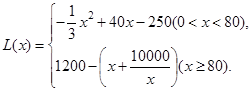
(2)当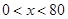 时,
时,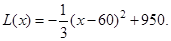
此时,当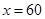 时,
时,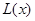 取得最大值
取得最大值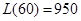 万元.
万元.
当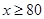 时,
时, 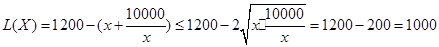
当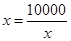 时,即
时,即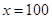 时
时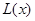 取得最大值1000万元.
取得最大值1000万元.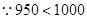
所以,当产量为100千件时,该厂在这一商品中所获利润最大,最大利润为1000万元.
考点:1.函数的实际应用,2.分段函数的解析式的求法,3.分段函数最大值的求解.


科目:高中数学 来源: 题型:解答题
某商品在近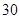 天内每件的销售价格
天内每件的销售价格 (元)与时间
(元)与时间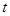 (天)的函数关系是
(天)的函数关系是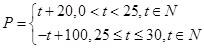 该商品的日销售量
该商品的日销售量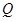 (件)与时间
(件)与时间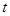 (天)的函数关系是
(天)的函数关系是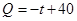
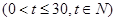 ,设商品的日销售额为
,设商品的日销售额为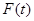 (销售量与价格之积)
(销售量与价格之积)
(1)求商品的日销售额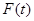 的解析式;
的解析式;
(2)求商品的日销售额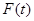 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知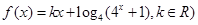 是偶函数.
是偶函数.
(1)求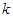 的值;
的值;
(2)证明:对任意实数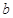 ,函数
,函数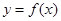 的图像与直线
的图像与直线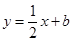 最多只有一个交点;
最多只有一个交点;
(3)设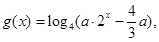 若函数
若函数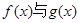 的图像有且只有一个公共点,求实数
的图像有且只有一个公共点,求实数 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
相关部门对跳水运动员进行达标定级考核,动作自选,并规定完成动作成绩在八分及以上的定为达标,成绩在九分及以上的定为一级运动员. 已知参加此次考核的共有56名运动员.
(1)考核结束后,从参加考核的运动员中随机抽取了8人,发现这8人中有2人没有达标,有3人为一级运动员,据此请估计此次考核的达标率及被定为一级运动员的人数;
(2)经过考核,决定从其中的A、B、C、D、E五名一级运动员中任选2名参加跳水比赛(这五位运动员每位被选中的可能性相同). 写出所有可能情况,并求运动员E被选中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
工厂生产某种产品,次品率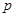 与日产量
与日产量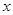 (万件)间的关系
(万件)间的关系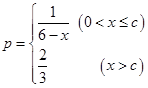 (
( 为常数,且
为常数,且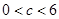 ),已知每生产一件合格产品盈利
),已知每生产一件合格产品盈利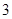 元,每出现一件次品亏损
元,每出现一件次品亏损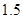 元.
元.
(1)将日盈利额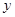 (万元)表示为日产量
(万元)表示为日产量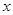 (万件)的函数;
(万件)的函数;
(2)为使日盈利额最大,日产量应为多少万件?(注:  )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com