
已知函数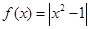 ,
,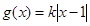 .
.
(Ⅰ)已知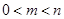 ,若
,若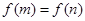 ,求
,求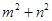 的值;
的值;
(Ⅱ)设 ,当
,当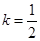 时,求
时,求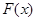 在
在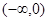 上的最小值;
上的最小值;
(Ⅲ)求函数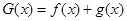 在区间
在区间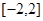 上的最大值.
上的最大值.
(Ⅰ)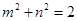 ;(Ⅱ)当
;(Ⅱ)当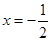 时,
时,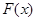 最小值为
最小值为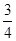 ;(Ⅲ)当
;(Ⅲ)当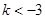 时,
时,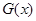 在
在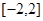 上的最大值为0;当
上的最大值为0;当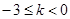 时,
时,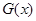 在
在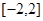 上的最大值为
上的最大值为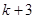 ;当
;当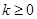 时,
时,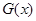 在
在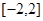 上的最大值为
上的最大值为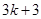 .
.
解析试题分析:(Ⅰ)将函数 去掉绝对值写成分段函数形式,结合函数图像满足
去掉绝对值写成分段函数形式,结合函数图像满足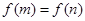 的
的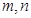 只可能为
只可能为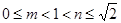 ,从而
,从而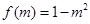 ,
,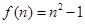 ,由
,由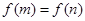 即可得
即可得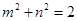 ;(Ⅱ)写出
;(Ⅱ)写出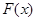 的表达式,根据分段函数的性质,先求出每一段上的最小值,其中最小的即为
的表达式,根据分段函数的性质,先求出每一段上的最小值,其中最小的即为 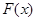 的最小值;(Ⅲ)将
的最小值;(Ⅲ)将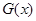 写成分段函数的形式,每一段均为二次函数的形式,结合二次函数图像,分类讨论函数的对称轴与区间的关系,从而求出最大值.
写成分段函数的形式,每一段均为二次函数的形式,结合二次函数图像,分类讨论函数的对称轴与区间的关系,从而求出最大值.
试题解析:(Ⅰ)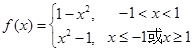
由 图像可知,
图像可知,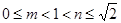
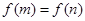 即为
即为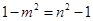 ,所以
,所以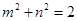 3分
3分
(Ⅱ)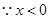 ,则
,则 ,
,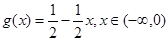
当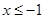 时,
时,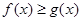 ,即为
,即为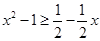 ,解得
,解得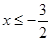
当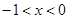 时,
时,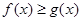 ,即为
,即为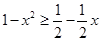 ,解得
,解得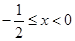
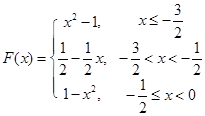
当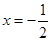 时,
时,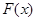 最小值为
最小值为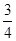
(本问也可直接利用图像说明理由求解) 6分
(Ⅲ)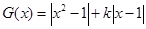
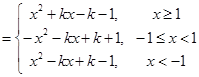
①记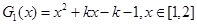 ,结合图像可知,
,结合图像可知,
当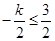 ,即
,即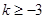 时,
时,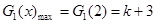
当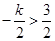 ,即
,即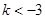 时,
时,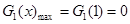 8分
8分
②记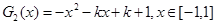 ,结合图像可知,
,结合图像可知,
当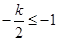 ,即
,即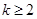 时,
时,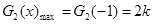
当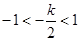 ,即
,即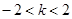 时,
时,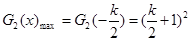 [来源:学*科*网Z*X*X*K]
[来源:学*科*网Z*X*X*K]
当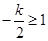 ,即
,即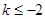 时,
时,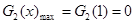
③记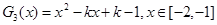 ,结合图像可知,
,结合图像可知,
当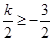 ,即
,即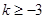 时,
时,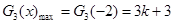
当 ,即
,即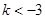 时,
时,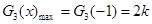 10分
10分
由上讨论可知:
当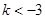 时,
时,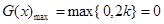
当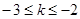 时,
时,
当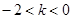 时,
时,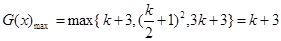
当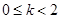 时,
时,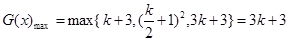
当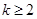 时,
时,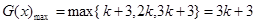 15分
15分
综上所述:当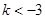 时,
时,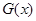 在
在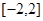 上的最大值为0
上的最大值为0
当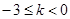 时,
时,

 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案科目:高中数学 来源: 题型:解答题
某种海洋生物身体的长度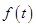 (单位:米)与生长年限t(单位:年)
(单位:米)与生长年限t(单位:年)
满足如下的函数关系: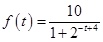 .(设该生物出生时t=0)
.(设该生物出生时t=0)
(1)需经过多少时间,该生物的身长超过8米;
(2)设出生后第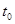 年,该生物长得最快,求
年,该生物长得最快,求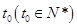 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(14分)已知函数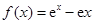 .
.
(Ⅰ)求函数 的最小值;
的最小值;
(Ⅱ)求证: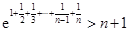
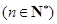 ;
;
(Ⅲ)对于函数 与
与 定义域上的任意实数
定义域上的任意实数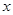 ,若存在常数
,若存在常数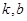 ,使得
,使得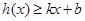 和
和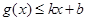 都成立,则称直线
都成立,则称直线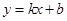 为函数
为函数 与
与 的“分界线”.设函数
的“分界线”.设函数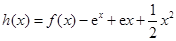 ,
,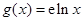 ,
, 与
与 是否存在“分界线”?若存在,求出
是否存在“分界线”?若存在,求出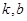 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
运货卡车以每小时 千米的速度匀速行驶130千米
千米的速度匀速行驶130千米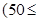
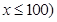 (单位:千米/小时).假设汽油的价格是每升2元,而汽车每小时耗油
(单位:千米/小时).假设汽油的价格是每升2元,而汽车每小时耗油 升,司机的工资是每小时14元.
升,司机的工资是每小时14元.
(1)求这次行车总费用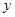 关于
关于 的表达式;
的表达式;
(2)当 为何值时,这次行车的总费用最低,并求出最低费用的值.
为何值时,这次行车的总费用最低,并求出最低费用的值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某公园准备建一个摩天轮,摩天轮的外围是一个周长为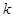 米的圆.在这个圆上安装座位,且每个座位和圆心处的支点都有一根直的钢管相连.经预算,摩天轮上的每个座位与支点相连的钢管的费用为
米的圆.在这个圆上安装座位,且每个座位和圆心处的支点都有一根直的钢管相连.经预算,摩天轮上的每个座位与支点相连的钢管的费用为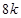 元/根,且当两相邻的座位之间的圆弧长为
元/根,且当两相邻的座位之间的圆弧长为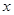 米时,相邻两座位之间的钢管和其中一个座位的总费用为
米时,相邻两座位之间的钢管和其中一个座位的总费用为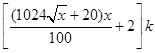 元.假设座位等距离分布,且至少有两个座位,所有座位都视为点,且不考虑其他因素,记摩天轮的总造价为
元.假设座位等距离分布,且至少有两个座位,所有座位都视为点,且不考虑其他因素,记摩天轮的总造价为 元.
元.
(Ⅰ)试写出 关于
关于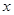 的函数关系式,并写出定义域;
的函数关系式,并写出定义域;
(Ⅱ)当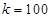 米时,试确定座位的个数,使得总造价最低?
米时,试确定座位的个数,使得总造价最低?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某工厂某种产品的年固定成本为250万元,每生产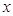 千件,需另投入成本为
千件,需另投入成本为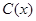 (万元),当年产量不足80千件时,
(万元),当年产量不足80千件时,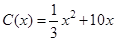 (万元).当年产量不小于80千件时,
(万元).当年产量不小于80千件时,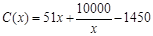 (万元).每件商品售价为500元.通过市场分析,该厂生产的商品能全部售完.
(万元).每件商品售价为500元.通过市场分析,该厂生产的商品能全部售完.
(1)写出年利润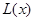 (万元)关于年产量
(万元)关于年产量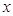 (千件)的函数解析式;
(千件)的函数解析式;
(2)年产量为多少千件时,该厂在这一商品的生产中所获利润最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com