
某种海洋生物身体的长度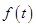 (单位:米)与生长年限t(单位:年)
(单位:米)与生长年限t(单位:年)
满足如下的函数关系: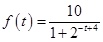 .(设该生物出生时t=0)
.(设该生物出生时t=0)
(1)需经过多少时间,该生物的身长超过8米;
(2)设出生后第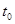 年,该生物长得最快,求
年,该生物长得最快,求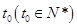 的值.
的值.
(1)6年;(2)4或5.
解析试题分析:(1)求需经过多少时间,该生物的身长超过8米,实质就是解不等式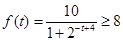 ,不等式解集中的最小值就是本题结论;(2)首先要搞懂什么是“长得最快”,“长得最快”就是说明这一年该生物身体增长的长度最大,因此实质就是求
,不等式解集中的最小值就是本题结论;(2)首先要搞懂什么是“长得最快”,“长得最快”就是说明这一年该生物身体增长的长度最大,因此实质就是求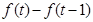 的最大值,即
的最大值,即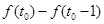 就是这个最大值,下面我们只要求出
就是这个最大值,下面我们只要求出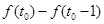 ,分析它的最大值是在
,分析它的最大值是在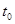 为何值时取得,
为何值时取得,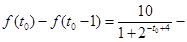
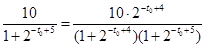 ,此式较繁,因此我们用换元法,设
,此式较繁,因此我们用换元法,设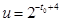 ,由有
,由有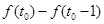
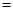
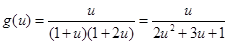 ,它的最大值求法一般是分子分母同时除以
,它的最大值求法一般是分子分母同时除以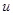 ,然后用基本不等式及不等式的性质得到结论.
,然后用基本不等式及不等式的性质得到结论.
试题解析:(1)设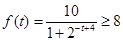 ,即
,即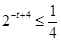 ,解得
,解得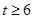 ,
,
即该生物6年后身长可超过8米; 5分
(2)设第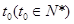 年生长最快,于是有
年生长最快,于是有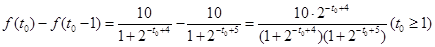 , 8分
, 8分
令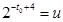 ,则
,则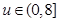 ,
,
令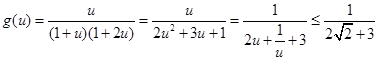 , 11分
, 11分
等号当且仅当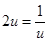 即
即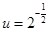 ,
, ,
,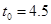 时成立,因为
时成立,因为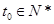 ,因此
,因此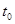 可能值为4或5,由
可能值为4或5,由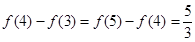 知,所求有年份为第4年和第5年,两年内各生长了
知,所求有年份为第4年和第5年,两年内各生长了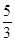 米. 14分
米. 14分
考点:(1)解不等式;(2)换元法与函数的最值.


科目:高中数学 来源: 题型:解答题
设函数f(x)=ax2+bx+b-1(a≠0).
(1)当a=1,b=-2时,求函数f(x)的零点;
(2)若对任意b∈R,函数f(x)恒有两个不同零点,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某种商品原来每件售价为25元,年销售8万件.
(1)据市场调查,若价格每提高1元,销售量将相应减少2000件,要使销售的总收入不低于原收入,该商品每件定价最多为多少元?
(2)为了扩大该商品的影响力,提高年销售量.公司决定明年对该商品进行全面技术革新和营销策略改革,并提高定价到 元.公司拟投入
元.公司拟投入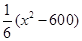 万元作为技改费用,投入50万元作为固定宣传费用,投入
万元作为技改费用,投入50万元作为固定宣传费用,投入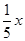 万元作为浮动宣传费用.试问:当该商品明年的销售量
万元作为浮动宣传费用.试问:当该商品明年的销售量 至少应达到多少万件时,才可能使明年的销售收入不低于原收入与总投入之和?并求出此时商品的每件定价.
至少应达到多少万件时,才可能使明年的销售收入不低于原收入与总投入之和?并求出此时商品的每件定价.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com