
【题目】已知关于x的函数y=(m+6)x2+2(m﹣1)x+m+1恒有零点.
(1)求m的范围;
(2)若函数有两个不同零点,且其倒数之和为﹣4,求m的值.
【答案】
(1)解:当m+6=0时,m=﹣6,函数为y=﹣14x﹣5显然有零点.
当m+6≠0时,m≠﹣6,由△=4(m﹣1)2﹣4(m+6)(m+1)=﹣36m﹣20≥0,得m≤﹣ ![]() .
.
∴当m≤﹣ ![]() 且m≠﹣6时,二次函数有零点.
且m≠﹣6时,二次函数有零点.
综上可得,m≤﹣ ![]() ,即m的范围为(﹣∞,﹣
,即m的范围为(﹣∞,﹣ ![]() ]
]
(2)解:设x1,x2是函数的两个零点,则有 x1+x2=﹣ ![]() ,x1x2=
,x1x2= ![]() .
.
∵ ![]() +
+ ![]() =﹣4,即
=﹣4,即 ![]() =﹣4,
=﹣4,
∴﹣ ![]() =﹣4,解得m=﹣3.
=﹣4,解得m=﹣3.
且当m=﹣3时,m+6≠0,△>0,符合题意,
∴m的值为﹣3
【解析】(1)当m+6=0时,即m=﹣6时,满足条件.当m+6≠0时,由≥0求得m≤﹣ ![]() 且m≠﹣6.综合可得m的范围.(2)设x1,x2是函数的两个零点,由条件并利用一元二次方程根与系数的关系求得m的值.
且m≠﹣6.综合可得m的范围.(2)设x1,x2是函数的两个零点,由条件并利用一元二次方程根与系数的关系求得m的值.
【考点精析】本题主要考查了二次函数的性质和函数的零点的相关知识点,需要掌握增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小;函数的零点就是方程的实数根,亦即函数的图象与轴交点的横坐标.即:方程有实数根,函数的图象与坐标轴有交点,函数有零点才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】某兴趣小组有9名学生.若从9名学生中选取3人,则选取的3人中恰好有一个女生的概率是 ![]() .
.
(1)该小组中男女学生各多少人?
(2)9个学生站成一列队,现要求女生保持相对顺序不变(即女生 前后顺序保持不变)重新站队,问有多少种重新站队的方法?(要求用数字作答)
(3)9名学生站成一列,要求男生必须两两站在一起,有多少种站队的方法?(要求用数字作答)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某种水箱用的“浮球”,是由两个半球和一个圆柱筒组成的.已知半球的直径是6 cm,圆柱筒高为2 cm.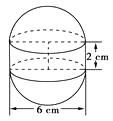
(1)这种“浮球”的体积是多少cm3(结果精确到0.1)?
(2)要在2 500个这样的“浮球”表面涂一层胶,如果每平方米需要涂胶100克,那么共需胶多少克?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设全集U=R,集合M={x||x﹣ ![]() |
| ![]() },P={x|﹣1≤x≤4},则(UM)∩P等于( )
},P={x|﹣1≤x≤4},则(UM)∩P等于( )
A.{x|﹣4≤x≤﹣2}
B.{x|﹣1≤x≤3}
C.{x|3<x≤4}
D.{x|3≤x≤4}
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com