
【题目】某学校研究性学习小组对该校高三学生视力情况进行调查,在高三的全体1000名学生中随机抽取了100名学生的体检表,学习小组成员发现,学习成绩突出的学生,近视的比较多,为了研究学生的视力与学习成绩是否有关系,对年级名次在1~50名和951~1000名的学生进行了调查,得到如下数据:
(1)根据表中的数据,能否在犯错的概率不超过0.05的前提下认为视力与学习成绩有关系?
(2)根据表中数据,在调查的100名学生中,按照分层抽样在不近视的学生中抽取了9人,进一步调查他们良好的护眼习惯,并且在这9人中任取3人,记名次在1~50名的学生人数为X,求X的分布列和数学期望.
年级名次 | 1~50 | 951~1000 |
近视 | 41 | 32 |
不近视 | 9 | 18 |
附:P(K2≥3.841=0.05)K2= ![]() .
.
 活力课时同步练习册系列答案
活力课时同步练习册系列答案科目:高中数学 来源: 题型:
【题目】已知:sin230°+sin290°+sin2150°= ![]() ,sin25°+sin265°+sin2125°=
,sin25°+sin265°+sin2125°= ![]() .通过观察上述两等式的规律,请你写出一般性的命题,并给出证明.
.通过观察上述两等式的规律,请你写出一般性的命题,并给出证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数y=f(x)是定义域为R的偶函数,当x≥0时,f(x)= 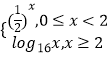 ,若关于x的方程[f(x)]2+af(x)﹣a﹣1=0(a∈R)有且只有7个不同实数根,则a的取值范围是 .
,若关于x的方程[f(x)]2+af(x)﹣a﹣1=0(a∈R)有且只有7个不同实数根,则a的取值范围是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是2012年在某大学自主招生考试的面试中,七位评委为某考生打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为( )
7 | 9 | ||||
8 | 4 | 4 | 6 | 4 | 7 |
9 | 3 |
A.84,4.84
B.84,1.6
C.85,1.6
D.85,4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设点M(x,y)在|x|≤1,|y|≤1时按均匀分布出现,试求满足:
(1)x+y≥0的概率;
(2)x+y<1的概率;
(3)x2+y2≥1的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知F为椭圆C: ![]() +
+ ![]() =1的右焦点,椭圆C上任意一点P到点F的距离与点P到直线l:x=m的距离之比为
=1的右焦点,椭圆C上任意一点P到点F的距离与点P到直线l:x=m的距离之比为 ![]() ,求:
,求:
(1)直线l方程;
(2)设A为椭圆C的左顶点,过点F的直线交椭圆C于D、E两点,直线AD、AE与直线l分别相交于M、N两点.以MN为直径的是圆是否恒过一定点,若是,求出定点坐标,若不是请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com