
【题目】已知F为椭圆C: ![]() +
+ ![]() =1的右焦点,椭圆C上任意一点P到点F的距离与点P到直线l:x=m的距离之比为
=1的右焦点,椭圆C上任意一点P到点F的距离与点P到直线l:x=m的距离之比为 ![]() ,求:
,求:
(1)直线l方程;
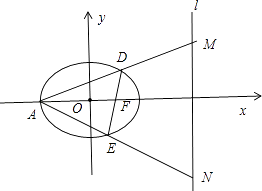
(2)设A为椭圆C的左顶点,过点F的直线交椭圆C于D、E两点,直线AD、AE与直线l分别相交于M、N两点.以MN为直径的是圆是否恒过一定点,若是,求出定点坐标,若不是请说明理由.
【答案】
(1)解:由椭圆C: ![]() +
+ ![]() =1,可得a=2,c=1,右焦点F(1,0),其离心率e=
=1,可得a=2,c=1,右焦点F(1,0),其离心率e= ![]() .
.
∵椭圆C上任意一点P到点F的距离与点P到直线l:x=m的距离之比为 ![]() ,
,
∴ ![]() =4.
=4.
∴直线l方程为:x=4
(2)解:当DE⊥x轴时,把x=1代入椭圆方程解得y= ![]() ,∴D
,∴D ![]() ,E
,E ![]() .
.
可得直线AD的方程:y= ![]() ,解得M(4,3),同理可得N(4,﹣3),
,解得M(4,3),同理可得N(4,﹣3),
可得以MN为直径的圆过点F(1,0),G(7,0).
下面证明以MN为直径的圆恒过上述两定点.
证明:设直线DE的方程为:my=x﹣1,D(x1,y1),E(x2,y2).
联立 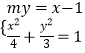 ,化为(3m2+4)y2+6my﹣9=0,
,化为(3m2+4)y2+6my﹣9=0,
∴y1+y2=﹣ ![]() ,y1y2=
,y1y2= ![]() .
.
直线AD的方程为:y= ![]() ,可得M
,可得M ![]() ,
,
同理可得N ![]() .
.
∴ ![]() =
= ![]()
![]() =9+
=9+ ![]()
=9+ 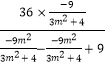 =9﹣9=0,
=9﹣9=0,
∴以MN为直径的圆恒过一定点F(1,0),G(7,0).
同理可证:以MN为直径的圆恒过一定点G(7,0).
因此以MN为直径的圆恒过一定点F(1,0),(7,0).
【解析】(1)利用椭圆的标准方程及其椭圆的第二定义即可得出;(2)当DE⊥x轴时,把x=1代入椭圆方程解得D ![]() ,E
,E ![]() .可得直线AD的方程:y=
.可得直线AD的方程:y= ![]() ,解得M,N,可得以MN为直径的圆过点F(1,0),G(7,0). 下面证明以MN为直径的圆恒过上述两定点.设直线DE的方程为:my=x﹣1,D(x1 , y1),E(x2 , y2).与椭圆方程联立化为(3m2+4)y2+6my﹣9=0,直线AD的方程为:y=
,解得M,N,可得以MN为直径的圆过点F(1,0),G(7,0). 下面证明以MN为直径的圆恒过上述两定点.设直线DE的方程为:my=x﹣1,D(x1 , y1),E(x2 , y2).与椭圆方程联立化为(3m2+4)y2+6my﹣9=0,直线AD的方程为:y= ![]() ,可得M
,可得M ![]() ,同理可得N
,同理可得N ![]() .利用根与系数的关系可证明
.利用根与系数的关系可证明 ![]() =0,即可得出结论.
=0,即可得出结论.


科目:高中数学 来源: 题型:
【题目】设a,b为两条直线,α,β为两个平面,下列四个命题中,正确的命题是( )
A.若a,b与α所成的角相等,则α∥b
B.若a∥α,b∥β,α∥β,则a∥b
C.若aα,bβ,α∥b,则α∥β
D.若a⊥α,b⊥β,α⊥β,是a⊥b
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校研究性学习小组对该校高三学生视力情况进行调查,在高三的全体1000名学生中随机抽取了100名学生的体检表,学习小组成员发现,学习成绩突出的学生,近视的比较多,为了研究学生的视力与学习成绩是否有关系,对年级名次在1~50名和951~1000名的学生进行了调查,得到如下数据:
(1)根据表中的数据,能否在犯错的概率不超过0.05的前提下认为视力与学习成绩有关系?
(2)根据表中数据,在调查的100名学生中,按照分层抽样在不近视的学生中抽取了9人,进一步调查他们良好的护眼习惯,并且在这9人中任取3人,记名次在1~50名的学生人数为X,求X的分布列和数学期望.
年级名次 | 1~50 | 951~1000 |
近视 | 41 | 32 |
不近视 | 9 | 18 |
附:P(K2≥3.841=0.05)K2= ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=cos(ωx+φ)(ω>0,﹣ ![]() <φ<0)的最小正周期为π,且f(
<φ<0)的最小正周期为π,且f( ![]() )=
)= ![]() .
.
(1)求ω和φ的值;
(2)求f(x)的单调递增区间;
(3)求f(x)在[0, ![]() ]上的值域.
]上的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={x|y= ![]() },B={x|log2x≤1},则A∩B=( )
},B={x|log2x≤1},则A∩B=( )
A.{x|﹣3≤x≤1}
B.{x|0<x≤1}
C.{x|﹣3≤x≤2}
D.{x|x≤2}
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com