
【题目】已知函数![]() .
.
(1)求函数![]() 的单调区间;
的单调区间;
(2)若![]() 恒成立,试确定实数
恒成立,试确定实数![]() 的取值范围;
的取值范围;
(3)证明![]() .
.
【答案】(1)函数![]() 的递增区间为
的递增区间为![]() ,函数
,函数![]() 的递减区间为
的递减区间为![]() ;(2)
;(2)![]() ;(3)见解析.
;(3)见解析.
【解析】试题分析:(1)先求导数![]() ,再确定导函数在定义区间上零点情况:当k≤0时,导函数恒大于零,为增函数;当k>0时,由一个零点x=
,再确定导函数在定义区间上零点情况:当k≤0时,导函数恒大于零,为增函数;当k>0时,由一个零点x=![]() ,先减后增(2)不等式恒成立问题,一般转化Wie对应函数最值问题,即
,先减后增(2)不等式恒成立问题,一般转化Wie对应函数最值问题,即![]() ,结合(1)的单调性情况,可得k>0且f(
,结合(1)的单调性情况,可得k>0且f(![]() )=ln
)=ln![]() ≤0解得k≥1,(3)利用导数证明不等式,一般方法为构造恰当函数,利用其增减性进行证明:因为k=1时,f(x)≤0恒成立,即ln(x﹣1)<x﹣2,令
≤0解得k≥1,(3)利用导数证明不等式,一般方法为构造恰当函数,利用其增减性进行证明:因为k=1时,f(x)≤0恒成立,即ln(x﹣1)<x﹣2,令![]() ,则
,则![]() ,代入叠加得证
,代入叠加得证
试题解析:(I)∵f(x)=ln(x﹣1)﹣k(x﹣1)+1,(x>1)
∴f′(x)=![]() ﹣k,
﹣k,
当k≤0时,f′(x)>0恒成立,故函数在(1,+∞)为增函数,
当k>0时,令f′(x)=0,得x=![]()
当f′(x)<0,即1<x<![]() 时,函数为减函数,
时,函数为减函数,
当f′(x)>0,即x>![]() 时,函数为增函数,
时,函数为增函数,
综上所述,当k≤0时,函数f(x)在(1,+∞)为增函数,
当k>0时,函数f(x)在(1,![]() )为减函数,在(
)为减函数,在(![]() ,+∞)为增函数.
,+∞)为增函数.
(Ⅱ)由(1)知,当k≤0时,f′(x)>0函数f(x)在定义域内单调递增,f(x)≤0不恒成立,
当k>0时,函数f(x)在(1,![]() )为减函数,在(
)为减函数,在(![]() ,+∞)为增函数.
,+∞)为增函数.
当x=![]() 时,f(x)取最大值,f(
时,f(x)取最大值,f(![]() )=ln
)=ln![]() ≤0
≤0
∴k≥1,即实数k的取值范围为[1,+∞)
(Ⅲ)由(2)知k=1时,f(x)≤0恒成立,即ln(x﹣1)<x﹣2
∴![]() <1﹣
<1﹣![]() ,
,
∵![]() =
=![]() =
=![]() <
<![]() =
=![]()
取x=3,4,5…n,n+1累加得
∴![]() +…+
+…+![]() <
<![]() +
+![]() +
+![]() +…+
+…+![]() =
=![]() ,(n∈N,n>1).
,(n∈N,n>1).


科目:高中数学 来源: 题型:
【题目】甲、乙两位同学玩游戏,对于给定的实数a1 , 按下列方法操作一次产生一个新的实数:由甲、乙同时各掷一枚均匀的硬币,如果出现两个正面朝上或两个反面朝上,则把a1乘以2后再减去12;如果出现一个正面朝上,一个反面朝上,则把a1除以2后再加上12,这样就可以得到一个新的实数a2 , 对实数a2仍按上述方法进行一次操作,又得到一个新的实数a3 , 当a3>a1 , 甲获胜,否则乙获胜,若甲获胜的概率为 ![]() ,则a1的取值范围是( )
,则a1的取值范围是( )
A.(﹣∞,12]
B.[24,+∞)
C.(12,24)
D.(﹣∞,12]∪[24,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知:sin230°+sin290°+sin2150°= ![]() ,sin25°+sin265°+sin2125°=
,sin25°+sin265°+sin2125°= ![]() .通过观察上述两等式的规律,请你写出一般性的命题,并给出证明.
.通过观察上述两等式的规律,请你写出一般性的命题,并给出证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是2012年在某大学自主招生考试的面试中,七位评委为某考生打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为( )
7 | 9 | ||||
8 | 4 | 4 | 6 | 4 | 7 |
9 | 3 |
A.84,4.84
B.84,1.6
C.85,1.6
D.85,4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设点M(x,y)在|x|≤1,|y|≤1时按均匀分布出现,试求满足:
(1)x+y≥0的概率;
(2)x+y<1的概率;
(3)x2+y2≥1的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为选拔参加“央视猜灯谜大赛”的队员,在校内组织猜灯谜竞赛.规定:第一阶段知识测试成绩不小于![]() 分的学生进入第二阶段比赛.现有
分的学生进入第二阶段比赛.现有![]() 名学生参加知识测试,并将所有测试成绩绘制成如下所示的频率分布直方图.
名学生参加知识测试,并将所有测试成绩绘制成如下所示的频率分布直方图.
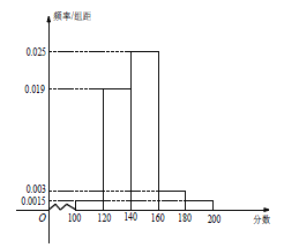
(1)估算这![]() 名学生测试成绩的中位数,并求进入第二阶段比赛的学生人数;
名学生测试成绩的中位数,并求进入第二阶段比赛的学生人数;
(2)将进入第二阶段的学生分成若干队进行比赛.现甲、乙两队在比赛中均已获得![]() 分,进入最后强答阶段.抢答规则:抢到的队每次需猜
分,进入最后强答阶段.抢答规则:抢到的队每次需猜![]() 条谜语,猜对
条谜语,猜对![]() 条得
条得![]() 分,猜错
分,猜错![]() 条扣
条扣![]() 分.根据经验,甲队猜对每条谜语的概率均为
分.根据经验,甲队猜对每条谜语的概率均为![]() ,乙队猜对每条谜语的概率均为
,乙队猜对每条谜语的概率均为![]() ,猜对第
,猜对第![]() 条的概率均为
条的概率均为![]() .若这两条抢到答题的机会均等,您做为场外观众想支持这两队中的优胜队,会把支持票投给哪队?
.若这两条抢到答题的机会均等,您做为场外观众想支持这两队中的优胜队,会把支持票投给哪队?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知F为椭圆C: ![]() +
+ ![]() =1的右焦点,椭圆C上任意一点P到点F的距离与点P到直线l:x=m的距离之比为
=1的右焦点,椭圆C上任意一点P到点F的距离与点P到直线l:x=m的距离之比为 ![]() ,求:
,求:
(1)直线l方程;
(2)设A为椭圆C的左顶点,过点F的直线交椭圆C于D、E两点,直线AD、AE与直线l分别相交于M、N两点.以MN为直径的是圆是否恒过一定点,若是,求出定点坐标,若不是请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() 为常数,e=2.71828…是自然对数的底数),曲线y=f(x)在点(1,f(1))处的切线与x轴平行. (Ⅰ)求k的值;
为常数,e=2.71828…是自然对数的底数),曲线y=f(x)在点(1,f(1))处的切线与x轴平行. (Ⅰ)求k的值;
(Ⅱ)求f(x)的单调区间;
(Ⅲ)设g(x)=(x2+x)f′(x),其中f′(x)为f(x)的导函数.证明:对任意x>0,g(x)<1+e﹣2 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com