
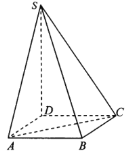
【题目】如图,四棱锥![]() 的底面是正方形,
的底面是正方形, ![]() 平面
平面![]() ,
,![]() ,点
,点![]() 是
是![]() 上的点,且
上的点,且![]() .
.
(1)求证:对任意的![]() ,都有
,都有![]() .
.
(2)设二面角C-AE-D的大小为![]() ,直线BE与平面
,直线BE与平面![]() 所成的角为
所成的角为![]() ,
,
若![]() ,求
,求![]() 的值.
的值.
【答案】(1)见解析; (2)![]() .
.
【解析】
(1)因为SD⊥平面ABCD,BD是BE在平面ABCD上的射影,由三垂线定理只要证AC
⊥BD即可.(2)先找出θ计算出cosθ,再找到![]() ,求出点O到BE的距离,再求出sin
,求出点O到BE的距离,再求出sin![]() ,解
,解
方程![]() 得到
得到![]() 的值.
的值.
(1)证明:连接BE、BD,由底面ABCD是正方形可得AC⊥BD.
∵SD⊥平面ABCD,∴BD是BE在平面ABCD上的射影,∴AC⊥BE
(2)解:由SD⊥平面ABCD知,∠DBE=φ,
∵SD⊥平面ABCD,CD平面ABCD,∴SD⊥CD.
又底面ABCD是正方形,∴CD⊥AD,而SD∩AD=D,CD⊥平面SAD.
连接AE、CE,过点D在平面SAD内作DF⊥AE于F,连接CF,则CF⊥AE,
故∠CFD是二面角C﹣AE﹣D的平面角,即∠CFD=θ.
在Rt△ADE中,∵AD=![]() a,DE=λa∴AE=a
a,DE=λa∴AE=a![]()
从而DF=![]() =
=![]()
在Rt△CDF中,tanθ=![]() =
=![]() ,所以
,所以![]() .
.
过点B作EO的垂线BG,因为AC⊥平面BDE,所以AC⊥BG,
所以∠BEO就是直线BE与平面![]() 所成的角
所成的角![]() ,
,
设点O到BE的距离为h,则由等面积得![]()
所以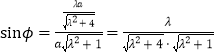 ,
,
因为![]() ,
,
所以![]() .
.


 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:高中数学 来源: 题型:
【题目】一盒中装有12个球,其中5个红球,4个黑球,2个白球,1个绿球.从中随机取出1球,求:
(1)取出1球是红球或黑球的概率;
(2)取出1球是红球或黑球或白球的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
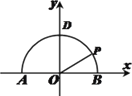
【题目】如图![]() 为半圆
为半圆![]() 的直径,点
的直径,点![]() 是半圆弧上的两点,
是半圆弧上的两点, ![]() ,
, ![]() .曲线
.曲线![]() 经过点
经过点![]() ,且曲线
,且曲线![]() 上任意点
上任意点![]() 满足:
满足: ![]() 为定值.
为定值.
(Ⅰ)求曲线![]() 的方程;
的方程;
(Ⅱ)设过点![]() 的直线
的直线![]() 与曲线
与曲线![]() 交于不同的两点
交于不同的两点![]() ,求
,求![]() 面积最大时的直线
面积最大时的直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设点![]() 是棱长为2的正方体
是棱长为2的正方体![]() 的棱
的棱![]() 的中点,点
的中点,点![]() 在面
在面![]() 所在的平面内,若平面
所在的平面内,若平面![]() 分别与平面
分别与平面![]() 和平面
和平面![]() 所成的锐二面角相等,则点
所成的锐二面角相等,则点![]() 到点
到点![]() 的最短距离是( )
的最短距离是( )
A. ![]() B.
B. ![]() C. 1 D.
C. 1 D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某产品生产厂家根据以往的生产销售经验得到下面有关生产销售的统计规律:每生产产品![]() (百台),其总成本为
(百台),其总成本为![]() (万元),其中固定成本为
(万元),其中固定成本为![]() 万元,并且每生产
万元,并且每生产![]() 百台的生产成本为
百台的生产成本为![]() 万元(总成本
万元(总成本![]() 固定成本
固定成本![]() 生产成本).销售收入
生产成本).销售收入![]() (万元)满足
(万元)满足![]() ,假定该产品产销平衡(即生产的产品都能卖掉),根据上述统计规律,请完成下列问题:
,假定该产品产销平衡(即生产的产品都能卖掉),根据上述统计规律,请完成下列问题:
(1)写出利润函数![]() 的解析式(利润
的解析式(利润![]() 销售收入
销售收入![]() 总成本);
总成本);
(2)工厂生产多少台产品时,可使盈利最多?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法错误的是( )
A. 命题![]() “
“![]() ”,则
”,则![]() :“
:“![]() ”
”
B. 命题“若![]() ,则
,则![]() ”的否命题是真命题
”的否命题是真命题
C. 若![]() 为假命题,则
为假命题,则![]() 为假命题
为假命题
D. 若![]() 是
是![]() 的充分不必要条件,则
的充分不必要条件,则![]() 是
是![]() 的必要不充分条件
的必要不充分条件
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com