练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】一盒中装有12个球，其中5个红球，4个黑球，2个白球，1个绿球．从中随机取出1球，求：

    (1)取出1球是红球或黑球的概率；

    (2)取出1球是红球或黑球或白球的概率．

    【答案】(1)取出球为红球或黑球的概率为 (2)取出球为红球或黑球或白球的概率为

    【解析】

    试题分析：思路一　(利用互斥事件求概率)记事件＝{任取球为红球}，＝{任取球为黑球}，

    ＝{任取球为白球}，＝{任取球为绿球}，根据题意知，事件彼此互斥，

    由互斥事件的概率公式即得

    思路二　(利用对立事件求概率)(1)由的对立事件为计算即得；

    (2)由的对立事件为，计算即得.

    试题解析：　方法一　(利用互斥事件求概率)

    记事件＝{任取球为红球}，＝{任取球为黑球}，

    ＝{任取球为白球}，＝{任取球为绿球}，

    则

    根据题意知，事件彼此互斥，

    由互斥事件的概率公式，得

    (1)取出球为红球或黑球的概率为

    (2)取出球为红球或黑球或白球的概率为

    方法二　(利用对立事件求概率)

    (1)由方法一知，取出球为红球或黑球的对立事件为取出球为白球或绿球，即的对立事件为，所以取出球为红球或黑球的概率为

    (2)因为的对立事件为，

    所以取出球为红球或黑球或白球的概率为

    .

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】某厂商调查甲、乙两种不同型号电视机在10个卖场的销售量（单位：台），并根据这10个卖场的销售情况，得到如图所示的茎叶图. 为了鼓励卖场，在同型号电视机的销售中，该厂商将销售量高于数据平均数的卖场命名为该型号电视机的“星级卖场”．

    （1）求在这10个卖场中，甲型号电视机的“星级卖场”的个数；

    （2）若在这10个卖场中，乙型号电视机销售量的平均数为26.7，求a>b的概率；

    （3）若a=1，记乙型号电视机销售量的方差为，根据茎叶图推断b为何值时，达到最值．

    （只需写出结论）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】若四面体的三组对棱分别相等，即

    给出下列结论：

    ①四面体每个面的面积相等；

    ②从四面体每个顶点出发的三条棱两两夹角之和大于 而小于 ；

    ③连结四面体每组对棱中点的线段相互垂直平分；

    ④从四面体每个顶点出发的三条棱的长可作为一个三角形的三边长；

    其中正确结论的序号是__________。（写出所有正确结论的序号）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某厂生产某种产品的年固定成本为250万元，每生产千件，需另投入成本，当年产量不足80千件时，（万元）；当年产量不小于80千件时（万元），通过市场分析，若每件售价为500元时，该厂本年内生产该商品能全部销售完．

    （1）写出年利润（万元）关于年产量（千件）的函数解析式；

    （2）年产量为多少千件时，该厂在这一商品的生产中所获的利润最大？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

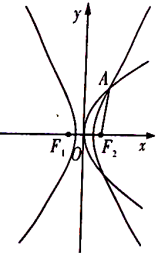
    【题目】如图，抛物线：与双曲线：（，）有公共焦点，点是曲线，在在第一象限的交点，且．

    （1）求双曲线的方程；

    （2）以为圆心的圆与双曲线的一条渐进线相切，圆．已知点，过点作互相垂直分别与圆、圆相交的直线和，设被圆解得的弦长为，被圆截得的弦长为．试探索是否为定值？请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图,在三棱柱ABC-A1B1C1中，已知AA1⊥底面ABC，AC⊥BC,四边形BB1C1C为正方形，设AB1的中点为D，B1C∩BC1=E.

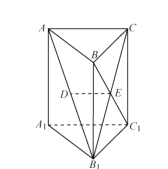
    求证：（1）DE∥平面AA1C1C;

    (2)BC1⊥平面AB1C.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某校高二奥赛班N名学生的物理测评成绩（满分120分）分布直方图如下，已知分数在100～110的学生数有21人。

    （Ⅰ）求总人数N和分数在110～115分的人数n;

    （Ⅱ）现准备从分数在110～115分的n名学生（女生占）中任选2人，求其中恰好含有一名女生的概率；

    （Ⅲ）为了分析某个学生的学习状态，对其下一阶段的学习提供指导性建议，对他前7次考试的数学成绩x（满分150分），物理成绩y进行分析，下面是该生7次考试的成绩。

    数学

    88

    83

    117

    92

    108

    100

    112

    物理

    94

    91

    108

    96

    104

    101

    106

    已知该生的物理成绩y与数学成绩x是线性相关的，若该生的数学成绩达到130分，请你估计他的物理成绩大约是多少？

    附：对于一组数据其回归线的斜率和截距的最小二乘估计分别为．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在锐角△ABC中，三个内角A，B，C所对的边分别为a，b，c，且acsin C＝(a2＋c2－b2)·sin B．

    (1)若C＝，求A的大小；

    (2)若a≠b，求的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

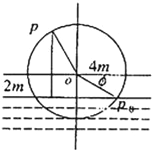
    【题目】如图，一个水轮的半径为4m，水轮圆心O距离水面2m，已知水轮每分钟转动5圈，如果当水轮上点P从水中浮现时（图中点p0）开始计算时间．

    （1）将点p距离水面的高度z（m）表示为时间t（s）的函数；

    （2）点p第一次到达最高点大约需要多少时间？

    查看答案和解析>>

    同步练习册答案