
【题目】某厂生产某种产品的年固定成本为250万元,每生产![]() 千件,需另投入成本
千件,需另投入成本![]() ,当年产量不足80千件时,
,当年产量不足80千件时,![]() (万元);当年产量不小于80千件时
(万元);当年产量不小于80千件时![]() (万元),通过市场分析,若每件售价为500元时,该厂本年内生产该商品能全部销售完.
(万元),通过市场分析,若每件售价为500元时,该厂本年内生产该商品能全部销售完.
(1)写出年利润![]() (万元)关于年产量
(万元)关于年产量![]() (千件)的函数解析式;
(千件)的函数解析式;
(2)年产量为多少千件时,该厂在这一商品的生产中所获的利润最大?
科目:高中数学 来源: 题型:
【题目】已知椭圆C的左、右焦点分别为![]() 、
、![]() ,且经过点
,且经过点![]()
(I)求椭圆C的方程:
(II)直线y=kx(k![]() R,k≠0)与椭圆C相交于A,B两点,D点为椭圆C上的动点,且|AD|=|BD|,请问△ABD的面积是否存在最小值?若存在,求出此时直线AB的方程:若不存在,说明理由.
R,k≠0)与椭圆C相交于A,B两点,D点为椭圆C上的动点,且|AD|=|BD|,请问△ABD的面积是否存在最小值?若存在,求出此时直线AB的方程:若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个盒中装有编号分别为1,2,3,4的四个形状大小完全相同的小球.
(1)从盒中任取两球,求取出的球的编号之和大于5的概率.
(2)从盒中任取一球,记下该球的编号![]() ,将球放回,再从盒中任取一球,记下该球的编号
,将球放回,再从盒中任取一球,记下该球的编号![]() ,求
,求![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高三共有2000名学生参加广安市联考,现随机抽取100名学生的成绩(单位:分),并列成如下表所示的频数分布表:
组别 |
|
|
|
|
|
|
频数 | 6 | 18 | 28 | 26 | 17 | 5 |
(1)试估计该年级成绩![]() 分的学生人数;
分的学生人数;
(2)已知样本中成绩在![]() 中的6名学生中,有4名男生,2名女生,现从中选2人进行调研,求恰好选中一名男生一名女生的概率.
中的6名学生中,有4名男生,2名女生,现从中选2人进行调研,求恰好选中一名男生一名女生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一盒中装有12个球,其中5个红球,4个黑球,2个白球,1个绿球.从中随机取出1球,求:
(1)取出1球是红球或黑球的概率;
(2)取出1球是红球或黑球或白球的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某服装商场为了了解毛衣的月销售量y(件)与月平均气温x(℃)之间的关系,随机统计了某4个月的月销售量与当月平均气温,其数据如下表:

(1) 算出线性回归方程![]() ; (a,b精确到十分位)
; (a,b精确到十分位)
(2)气象部门预测下个月的平均气温约为3℃,据此估计,求该商场下个月毛衣的销售量.
(参考公式: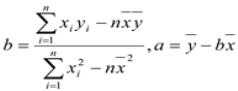 )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com