
【题目】如图,抛物线![]() :
:![]() 与双曲线
与双曲线![]() :
:![]() (
(![]() ,
,![]() )有公共焦点
)有公共焦点![]() ,点
,点![]() 是曲线
是曲线![]() ,
,![]() 在在第一象限的交点,且
在在第一象限的交点,且![]() .
.
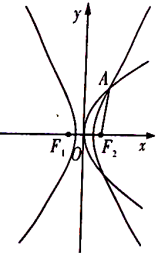
(1)求双曲线![]() 的方程;
的方程;
(2)以![]() 为圆心的圆
为圆心的圆![]() 与双曲线的一条渐进线相切,圆
与双曲线的一条渐进线相切,圆![]() .已知点
.已知点![]() ,过点
,过点![]() 作互相垂直分别与圆
作互相垂直分别与圆![]() 、圆
、圆![]() 相交的直线
相交的直线![]() 和
和![]() ,设
,设![]() 被圆
被圆![]() 解得的弦长为
解得的弦长为![]() ,
,![]() 被圆
被圆![]() 截得的弦长为
截得的弦长为![]() .试探索
.试探索![]() 是否为定值?请说明理由.
是否为定值?请说明理由.
 金钥匙试卷系列答案
金钥匙试卷系列答案科目:高中数学 来源: 题型:
【题目】已知A(4,-3),B(2,-1)和直线l:4x+3y-2=0.
(1)求在直角坐标平面内满足|PA|=|PB|的点P的方程;
(2)求在直角坐标平面内一点P满足|PA|=|PB|且点P到直线l的距离为2的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在高为2的梯形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,过
,过![]() 、
、![]() 分别作
分别作![]() ,
, ![]() ,垂足分别为
,垂足分别为![]() 、
、![]() 。已知
。已知![]() ,将梯形
,将梯形![]() 沿
沿![]() 、
、![]() 同侧折起,得空间几何体
同侧折起,得空间几何体![]() ,如图2。
,如图2。

(1)若![]() ,证明:
,证明: ![]() ;
;
(2)若![]() ,证明:
,证明: ![]() ;
;
(3)在(1),(2)的条件下,求三棱锥![]() 的体积。
的体积。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高三共有2000名学生参加广安市联考,现随机抽取100名学生的成绩(单位:分),并列成如下表所示的频数分布表:
组别 |
|
|
|
|
|
|
频数 | 6 | 18 | 28 | 26 | 17 | 5 |
(1)试估计该年级成绩![]() 分的学生人数;
分的学生人数;
(2)已知样本中成绩在![]() 中的6名学生中,有4名男生,2名女生,现从中选2人进行调研,求恰好选中一名男生一名女生的概率.
中的6名学生中,有4名男生,2名女生,现从中选2人进行调研,求恰好选中一名男生一名女生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2017年天猫五一活动结束后,某地区研究人员为了研究该地区在五一活动中消费超过3000元的人群的年龄状况,随机在当地消费超过3000元的群众中抽取了500人作调查,所得概率分布直方图如图所示:记年龄在![]() ,
, ![]() ,
, ![]() 对应的小矩形的面积分别是
对应的小矩形的面积分别是![]() ,且
,且![]() .
.
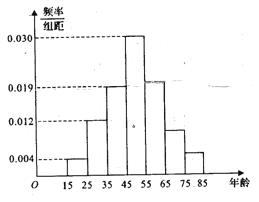
(1)以频率作为概率,若该地区五一消费超过3000元的有30000人,试估计该地区在五一活动中消费超过3000元且年龄在![]() 的人数;
的人数;
(2)计算在五一活动中消费超过3000元的消费者的平均年龄;
(3)若按照分层抽样,从年龄在![]() ,
, ![]() 的人群中共抽取7人,再从这7人中随机抽取2人作深入调查,求至少有1人的年龄在
的人群中共抽取7人,再从这7人中随机抽取2人作深入调查,求至少有1人的年龄在![]() 内的概率.
内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一盒中装有12个球,其中5个红球,4个黑球,2个白球,1个绿球.从中随机取出1球,求:
(1)取出1球是红球或黑球的概率;
(2)取出1球是红球或黑球或白球的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前n项和为Sn,点
的前n项和为Sn,点![]() 在直线
在直线![]() 上,数列
上,数列![]() 为等差数列,且
为等差数列,且![]() ,前9项和为153.
,前9项和为153.
(1)求数列![]() 、
、![]() 的通项公式;
的通项公式;
(2)设![]() ,数列
,数列![]() 的前n项和为
的前n项和为![]() ,求使不等式
,求使不等式![]() 对一切的
对一切的![]() 都成立的最大整数k.
都成立的最大整数k.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】公差不为零的等差数列{an}中,a3=7,且a2,a4,a9成等比数列.
(1)求数列{an}的通项公式;
(2)设bn=![]() ,求数列{bn}的前n项和Sn.
,求数列{bn}的前n项和Sn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)=![]() (m>0,n>0).
(m>0,n>0).
(1) 当m=n=1时,求证:f(x)不是奇函数;
(2) 设f(x)是奇函数,求m与n的值;
(3) 在(2)的条件下,求不等式f(f(x))+f![]() <0的解集.
<0的解集.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com