
【题目】已知A(4,-3),B(2,-1)和直线l:4x+3y-2=0.
(1)求在直角坐标平面内满足|PA|=|PB|的点P的方程;
(2)求在直角坐标平面内一点P满足|PA|=|PB|且点P到直线l的距离为2的坐标.
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:(1)由题意可知|PA|=|PB|即点P为线段AB的中垂线,所过点P的轨迹为过AB中点,斜率满足![]() 。(2)由(1)可知点P的方程x-y-5=0,
。(2)由(1)可知点P的方程x-y-5=0,
设点P的坐标为(a,b),再由点到直线的距离公式和点在直线x-y-5=0,列方程组可解。
试题解析:(1)∵A(4,-3),B(2,-1),
∴线段AB的中点M的坐标为(3,-2),又![]()
∴线段AB的垂直平分线方程为y+2=x-3,
即点P的方程x-y-5=0.
(2)设点P的坐标为(a,b),
∵点P(a,b)在上述直线上,∴a-b-5=0.①
又点P(a,b)到直线l:4x+3y-2=0的距离为2,
∴![]() =2,即4a+3b-2=±10,②
=2,即4a+3b-2=±10,②
联立①②可得![]() 或
或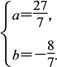
∴所求点P的坐标为(1,-4)或![]() .
.


科目:高中数学 来源: 题型:
【题目】某单位每天的用电量![]() (度)与当天最高气温
(度)与当天最高气温![]() (℃)之间具有线性相关关系,下表是该单位随机统计4天的用电量与当天最高气温的数据.
(℃)之间具有线性相关关系,下表是该单位随机统计4天的用电量与当天最高气温的数据.
最高气温(℃) | 26 | 29 | 31 | 34 |
用电量 (度) | 22 | 26 | 34 | 38 |
(Ⅰ)根据表中数据,求出回归直线的方程![]() (其中
(其中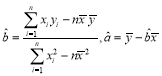 );
);
(Ⅱ)试预测某天最高气温为33℃时,该单位当天的用电量(精确到1度).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】重庆因夏长酷热多伏旱而得名“火炉”,八月是重庆最热、用电量最高的月份.下图是沙坪坝区居民八月份用电量(单位:度)的频率分布直方图,其分组区间依次为:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.

(1)求直方图中的![]() ;
;
(2)根据直方图估计八月份用电量的众数和中位数;
(3)在用电量为![]() ,
,![]() ,
,![]() ,
,![]() 的四组用户中,用分层抽样的方法抽取11户居民,则用电量在
的四组用户中,用分层抽样的方法抽取11户居民,则用电量在![]() 的用户应抽取多少户?
的用户应抽取多少户?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,ABC﹣A1B1C1是底面边长为2,高为![]() 的正三棱柱,经过AB的截面与上底面相交于PQ,设C1P=λC1A1(0<λ<1).
的正三棱柱,经过AB的截面与上底面相交于PQ,设C1P=λC1A1(0<λ<1).

(Ⅰ)证明:PQ∥A1B1;
(Ⅱ)当![]() 时,在图中作出点C在平面ABQP内的正投影F(说明作法及理由),并求四面体CABF的体积.
时,在图中作出点C在平面ABQP内的正投影F(说明作法及理由),并求四面体CABF的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂商调查甲、乙两种不同型号电视机在10个卖场的销售量(单位:台),并根据这10个卖场的销售情况,得到如图所示的茎叶图. 为了鼓励卖场,在同型号电视机的销售中,该厂商将销售量高于数据平均数的卖场命名为该型号电视机的“星级卖场”.
(1)求在这10个卖场中,甲型号电视机的“星级卖场”的个数;
(2)若在这10个卖场中,乙型号电视机销售量的平均数为26.7,求a>b的概率;
(3)若a=1,记乙型号电视机销售量的方差为![]() ,根据茎叶图推断b为何值时,
,根据茎叶图推断b为何值时,![]() 达到最值.
达到最值.
(只需写出结论)

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂为了对新研发的产品进行合理定价,将该产品按事先拟定的价格进行试销,得到一组检测数据![]() (
(![]() …
…![]() )如下表所示:
)如下表所示:
试销价格
| 4 | 5 | 6 | 7 |
| 9 |
产品销量
|
| 84 | 83 | 80 | 75 | 68 |
已知变量![]() 具有线性负相关关系,且
具有线性负相关关系,且![]() ,
,![]() ,现有甲、乙、丙三位同学通过计算求得其回归直线方程分别为:甲
,现有甲、乙、丙三位同学通过计算求得其回归直线方程分别为:甲![]() ,乙
,乙![]() ,丙
,丙![]() ,其中有且仅有一位同学的计算结果是正确的( ).
,其中有且仅有一位同学的计算结果是正确的( ).
(1)试判断谁的计算结果正确?并求出![]() 的值;
的值;
(2)若由线性回归方程得到的估计数据与检测数据的误差不超过1,则该检测数据是“理想数据”,现从检测数据中随机抽取2个,![]() 为“理想数据”的个数,求随机变量
为“理想数据”的个数,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,抛物线![]() :
:![]() 与双曲线
与双曲线![]() :
:![]() (
(![]() ,
,![]() )有公共焦点
)有公共焦点![]() ,点
,点![]() 是曲线
是曲线![]() ,
,![]() 在在第一象限的交点,且
在在第一象限的交点,且![]() .
.
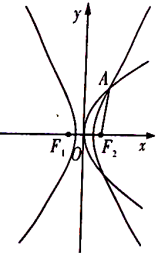
(1)求双曲线![]() 的方程;
的方程;
(2)以![]() 为圆心的圆
为圆心的圆![]() 与双曲线的一条渐进线相切,圆
与双曲线的一条渐进线相切,圆![]() .已知点
.已知点![]() ,过点
,过点![]() 作互相垂直分别与圆
作互相垂直分别与圆![]() 、圆
、圆![]() 相交的直线
相交的直线![]() 和
和![]() ,设
,设![]() 被圆
被圆![]() 解得的弦长为
解得的弦长为![]() ,
,![]() 被圆
被圆![]() 截得的弦长为
截得的弦长为![]() .试探索
.试探索![]() 是否为定值?请说明理由.
是否为定值?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com