
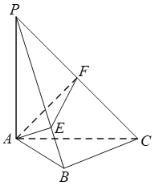
【题目】在《九章算术》中,将四个面都为直角三角形的四面体称之为鳖臑.如图,在鳖臑![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,且
,且![]() ,过点
,过点![]() 分别作
分别作![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,连结
,连结![]() ,当
,当![]() 的面积最大时,
的面积最大时,![]() __________.
__________.
【答案】![]()
【解析】
利用![]() 平面
平面![]() ,根据线面垂直的性质定理可得
,根据线面垂直的性质定理可得![]() ,结合已知,利用线面垂直的判定定理可以证明出
,结合已知,利用线面垂直的判定定理可以证明出![]() 平面
平面![]() ,进而可以证明出
,进而可以证明出![]() ,再结合已知,利用线面垂直的判定定理可以证明
,再结合已知,利用线面垂直的判定定理可以证明![]() 平面
平面![]() ,因此可以证明出
,因此可以证明出![]() ,最后利用线面垂直定理证明出
,最后利用线面垂直定理证明出![]() 平面
平面![]() ,因此得到
,因此得到![]() ,
,![]() ,且
,且![]() 为
为![]() 中点.
中点.
解法1:
设![]() ,
,![]() ,利用三角形面积公式可以求出
,利用三角形面积公式可以求出![]() 的长,在利用
的长,在利用![]() ,求出
,求出![]() 的长,最后求出
的长,最后求出![]() 的面积表达式,利用换元法和配方法求出
的面积表达式,利用换元法和配方法求出![]() 面积平方的最大值,最后求出
面积平方的最大值,最后求出![]() 的值;
的值;
解法2:
设![]() ,求出
,求出![]() 、
、![]() 、
、![]() 、
、![]() 的大小,再求出
的大小,再求出![]() 的大小,最后求出
的大小,最后求出
![]() 表达式,利用同角三角函数的关系中商关系和基本不等式求出最大值,根据等号成立的条件求出
表达式,利用同角三角函数的关系中商关系和基本不等式求出最大值,根据等号成立的条件求出![]() 的值.
的值.
因为![]() 平面
平面![]() ,所以
,所以![]() ,又
,又![]() ,
,
所以![]() 平面
平面![]() ,所以
,所以![]() ,又
,又![]() ,
,
所以![]() 平面
平面![]() ,所以
,所以![]() ,又
,又![]() ,
,
所以![]() 平面
平面![]() ,综上
,综上![]() ,
,![]() ,且
,且![]() 为
为![]() 中点.
中点.
解法1:
设![]() ,
,![]() ,则
,则![]() ,又
,又![]() ,则
,则![]() ,
,
又![]() ,可得
,可得![]() ,所以
,所以![]() ,
,
所以 ,令
,令![]() ,
,
则![]()
所以当![]() 时即
时即![]() ,
,![]() ,
,![]() ,此时
,此时 ,故填
,故填![]() .
.
解法2.
设![]() ,则
,则 ,所以
,所以![]() .
.
又![]() ,
,![]() ,所以
,所以![]() ,所以
,所以
所以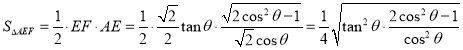
![]()
当且仅当![]() 即
即![]() 时,取等号.
时,取等号.
故答案为:![]()


 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,椭圆
,椭圆![]() :
:![]() 经过点
经过点![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设点![]() 是椭圆
是椭圆![]() 上的任意一点,射线
上的任意一点,射线![]() 与椭圆
与椭圆![]() 交于点
交于点![]() ,过点
,过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 有且只有一个公共点,直线
有且只有一个公共点,直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两个相异点,证明:
两个相异点,证明:![]() 面积为定值.
面积为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】南北朝时期杰出的数学家祖冲之的儿子祖暅在数学上也有很多创造,其最著名的成就是祖暅原理:夹在两个平行平面之间的几何体,被平行于这两个平面的任意平面所截,如果截得的两个截面的面积总相等,那么这两个几何体的体积相等,现有一个圆柱体和一个长方体,它们的底面面积相等,高也相等,若长方体的底面周长为![]() ,圆柱体的体积为
,圆柱体的体积为![]() ,根据祖暅原理,可推断圆柱体的高( )
,根据祖暅原理,可推断圆柱体的高( )
A.有最小值![]() B.有最大值
B.有最大值![]() C.有最小值
C.有最小值![]() D.有最大值
D.有最大值![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,以坐标原点为中心,以坐标轴为对称轴的椭圆C经过点M(2,1),N(![]() ,-
,-![]() ).
).
(1)求椭圆C的标准方程;
(2)经过点M作倾斜角互补的两条直线,分别与椭圆C相交于异于M点的A,B两点,求直线AB的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-4:坐标系与参数方程]
在直角坐标系中,以原点为极点,![]() 轴的正半轴为极轴建立极坐标系,已知曲线
轴的正半轴为极轴建立极坐标系,已知曲线![]() :
:![]() ,过点
,过点![]() 的直线
的直线![]() 的参数方程为:
的参数方程为:![]() (
(![]() 为参数),直线
为参数),直线![]() 与曲线
与曲线![]() 分别交于
分别交于![]() 、
、![]() 两点.
两点.
(1)写出曲线![]() 的直角坐标方程和直线
的直角坐标方程和直线![]() 的普通方程;
的普通方程;
(2)求线段![]() 的长和
的长和![]() 的积.
的积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,以坐标原点
中,以坐标原点![]() 务极点,
务极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() ,
,![]()
(1)求曲线![]() ,
,![]() 的直角坐标方程;
的直角坐标方程;
(2)曲线![]() 和
和![]() 的交点为
的交点为![]() ,
,![]() ,求以
,求以![]() 为直径的圆与
为直径的圆与![]() 轴的交点坐标.
轴的交点坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com